![[SLAM] 4. 3D-2D geometry, Triangulation, PnP](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F6fCGu%2FbtrSF9jSK2R%2FQE8xInxrt0eBk0DxkdkOKk%2Fimg.png)
안녕하세요. 후니대디입니다.
지난번에는 2D-2D geometry로 Essential Matrix, Fundamental Matrix에 관해 다루어봤습니다. 즉, Two view가 존재할때 (stereo 혹은 sequenced frame) two view간의 관계를 설명해보았습니다.
[SLAM] 3. 2D-2D geometry, Epipolar Geometry
안녕하세요. 후니대디입니다. 이번 포스팅은 2D-2D (two view) camera geometry에 대해서 살펴보겠습니다. Camera Model 시작하기전에 camera model 먼저 살펴보겠습니다. 3D world의 points를 2D image plane에 매핑하는
jaehoon-daddy.tistory.com
이번에는 3D-2D geometry에 관해 다루어보겠습니다.
전제적인 흐름을 요약해보면 지난 포스팅에서 언급한 Essential Matrix를 통해 two view relation을 구하고 이를 바탕으로 다시 오늘 다룰 Triangulation을 통해 3D상의 map point를 구합니다. 이 후에는 PnP방법을 통해 map point(3D)와 2D point와의 관계를 다시 구하게 됩니다. 이후에는 essential matrix가 아닌 pnp방법을 통해 pose tracking을 합니다.
Triangulation
앞선 포스팅에서 설명한 Essential Matrix를 통해 camera motion을 추정한 후 다음 단계는 Triangulation을 통해 map point(depth)를 추정하는 것입니다.
위의 그림에서 p1,p2과의 관계를 다시 한번 수식으로 나타내보면 $s_1x_1 = s_2Rx_2+t$로 표현할 수 있습니다. R,T는 Essential Matrix를 통해 구할 수 있고 그렇다면 scale(depth)인 $s_1, s_2$를 구할 수 있습니다.
양변에 $x_{1}^{s}$ skew_matrix를 곱합니다.
정리하면 $s_{1}x_{1}^{s}x_{1}=0=s_2x_{1}^{s}Rx_2+x_{1}^{s}t$로 나타낼 수 있습니다. 좌변이 0이 되는 이유는 $x_1 \times x_1$ 본인의 외적은 0이기 때문입니다. 이렇게 $s_2$를 구하면 $s_1$또한 쉽게 구할 수 있습니다.
하지만 실제 환경에서는 많은 noise가 있기 때문에 $s_1x_1 = s_2Rx_2+t$가 성립되지 않습니다.(위의 그림 참고)
따라서 $cost function = s_1x_1 - s_2Rx_2+t$로 설정하고 최소제곱해를 찾는 것이 일반적입니다.
PnP
PnP는 perspective-n-point의 줄임말로 위의 그림처럼 triangulation을 통해 구한 3D map point(depth)와 2D사이의 대응 관계가 주어졌을때 camera motion을 추정합니다. Essential Matrix를 구하는 것과 다르게 3~5개의 point pairs만 알면 camera motion을 추정할 수 있습니다. 때문에 mono cam의 경우에 초기 initialization을 위해 Essential Matrix를 사용한 이후에는 PnP를 통해 Camera Motion을 추정합니다.
OpenCV: Perspective-n-Point (PnP) pose computation
Pose computation overview The pose computation problem [166] consists in solving for the rotation and translation that minimizes the reprojection error from 3D-2D point correspondences. The solvePnP and related functions estimate the object pose given a se
docs.opencv.org
1. Direct Linear Transform(DLT)
SVD를 이용하여 해를 구하는 부분은 이전 포스팅을 참고하세요
[mathematic] SVD, 특이값분해
정의 우선 특이값(singular value)의 정의부터 보면, 임의의 행렬 A(mxn)의 특이값(singular value)는 $A^{T}A$에 대한 교윳값의 양의 제곱근입니다. SingularValue Decomposition(SVD)는 mxn차원의 행렬A에 대해 위에서
jaehoon-daddy.tistory.com
2. P3P
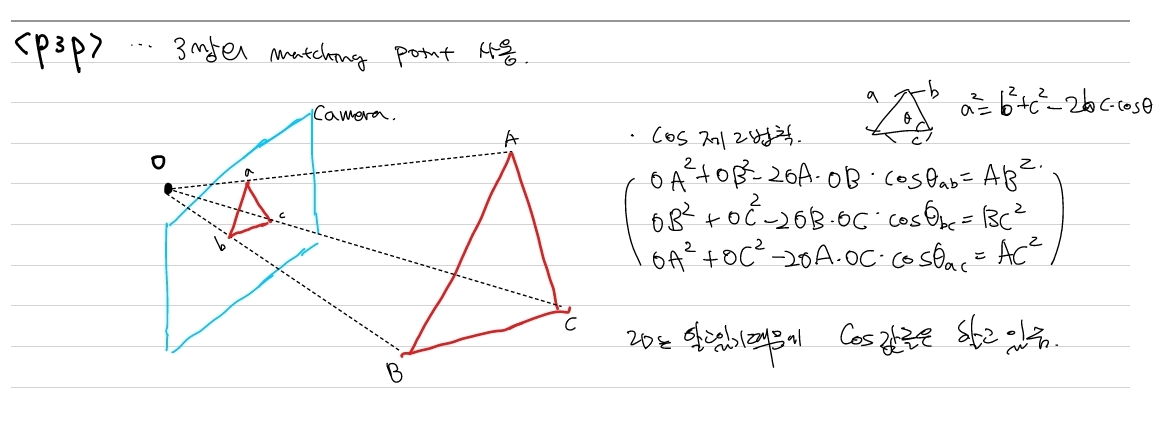
3. 실제적으로는 noise들에 robust해야하기 때문에 위의 p3p, DLT방법은 거의 사용하지 않습니다. EPnP, UPnP를 많이 사용합니다.(opencv는 이를 사용합니다.)
아래는 최근에 publish된 Neural Net을 이용한 방법입니다.
GitHub - tjiiv-cprg/EPro-PnP: [CVPR 2022 Oral, Best Student Paper] EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-
[CVPR 2022 Oral, Best Student Paper] EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation - GitHub - tjiiv-cprg/EPro-PnP: [CVPR 2022 Oral, Best S...
github.com
여기까지 3D-2D geometry, triangulation을 보았습니다.
이쯤에서 SLAM의 FE의 structure를 정리해보면 indirect method의 경우 feature를 추출하고(hand craft 방법으로 ORB, SIFT 이 있습니다.) 2D-2D geometry(essential matrix)로 initialization(mono cam인 경우)후에 이번에 포스팅한 triangulation으로 depth를 추정하고 이후 추정된 3D map point와 image feature간의 관계를 통해(PnP) camera motion을 추정해갑니다.
이후에는 BE에 관해 다뤄보겠습니다.
