[SLAM] 3. 2D-2D geometry, Epipolar Geometry

안녕하세요. 후니대디입니다.

이번 포스팅은 2D-2D (two view) camera geometry에 대해서 살펴보겠습니다.

---

Camera Model

 시작하기전에 camera model 먼저 살펴보겠습니다. 3D world의 points를 2D image plane에 매핑하는 프로세스에서 언급한 camera model을 사용합니다. 기본적으로 camera model은 pinhole model입니다. (광각렌즈 등을 사용하면 pinhole model에 맞지 않습니다.) pinhole camera model을 통해 카메라의 intrinsic parameter를 구할 수 있습니다.

 아래는 pinhole camera model 사진입니다. 빛의 직진성, 그리고 핀홀에만 빛이 투과된다는 가정에서 이루어집니다.

pinhole camera model

 intrinsic parameter는 카메라 구입시 Data Sheet등에 명기되어있지만, 시간이 지나면서 보통 틀어지기 때문에 체커보드 등을 통해서 카메라 실행하기 전에 calibration을 거쳐서 intrinsic parameter를 구해줍니다.

 이로써 저번 포스팅에서 설명한 좌표변환(extrinsic)과 위의 설명한 카메라 파라미터(intrinsic)을 통해 3D 물체가 2D camera plane 의 이르는 과정을 설명할 수 있습니다. 하나의 식으로 정리하면 아래와 같습니다.

extrinsic, intrinsic parameter

 풀어 말하면 world 좌표계 기준의 3D points 위치를 이전 포스팅에서 설명드린 (R|T) Homogenous coordinate을 이용하여 camera 좌표계 기준으로 나타냅니다. camera coordinate 기준으로 변경된 점을 위에서 설명한 projection과정을 통해 (camera intrinsic) image plane상의 위치를 추정할 수 있습니다.

*추가 부족한 부분은 아래 블로그 참고하시면 좋습니다.

What are Intrinsic and Extrinsic Camera Parameters in Computer Vision?

---

2D-2D: Epipolar Geometry

 이제는 single view가 아닌 two view를 살펴보겠습니다. 2D-2D pair의 대표적인 camera geometry로는 Epipolar Geometry가 있습니다. 두 장의 이미지에서 (두 장의 이미지는 시간의 흐름에 따라 연속적으로 찍은 사진일 수도 있고, Stereo와 같이 고정된 두개의 카메라렌즈에서 얻은 이미지 일 수도 있습니다.) SIFT, ORB와 같은 특징점을 추출하여 매칭한 매칭점들을 이용하여 2장의 이미지 사이의 기하하적인 관계를 표현하는 방법입니다.

 아래 그림의 2개의 frame과 3D point가 이루는 epipolar plane과 이에 대응되는 매칭점 사이의 fundametal matrix에 대해 유도해보았습니다.

Fundamental Matrix

 

epipolar geometry

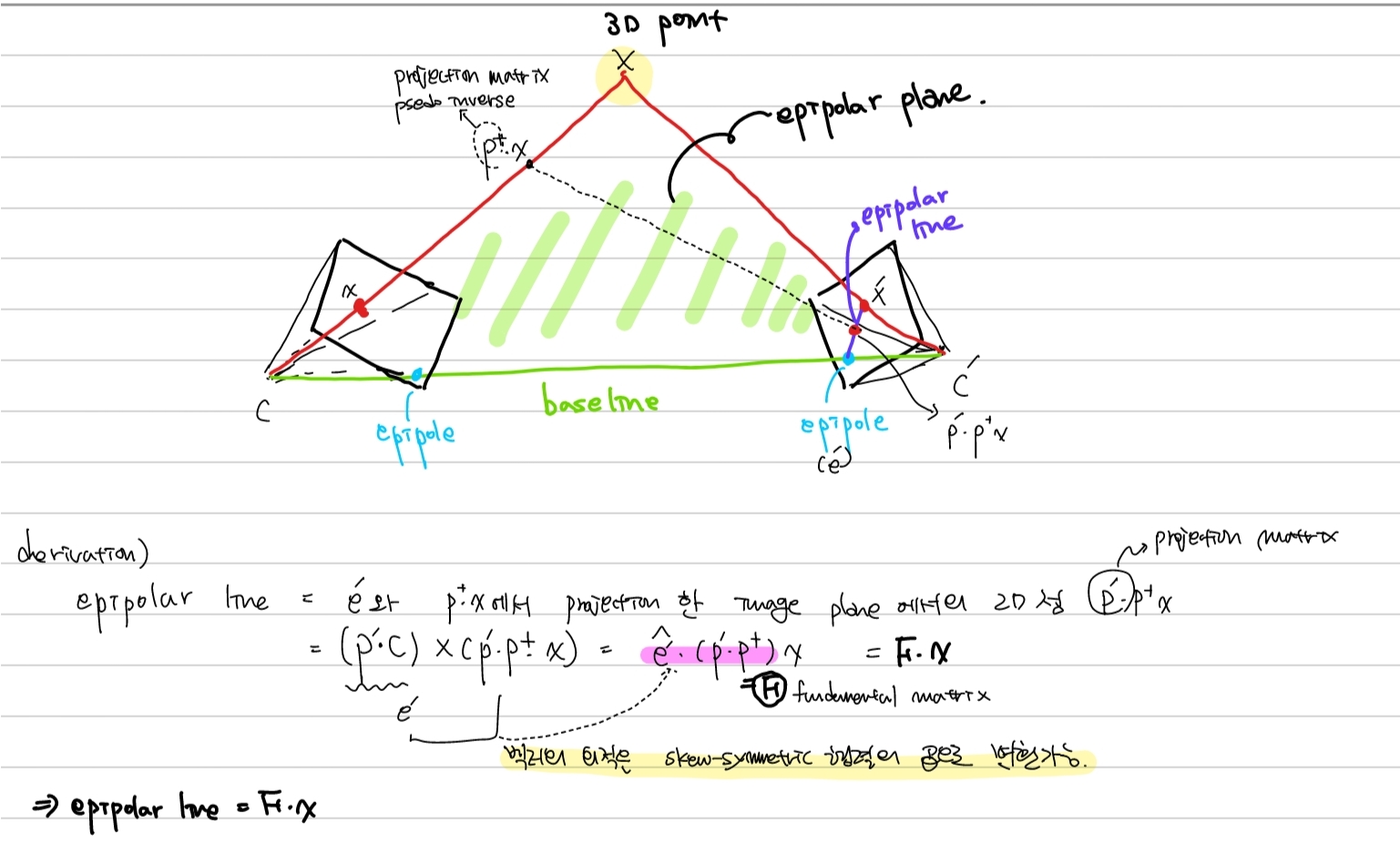
위의 Fx는 epipolar line,즉 직선이 되고 직선 위의 점 x'와의 내적은 0이 됩니다. 

따라서 최종 정리하면 아래와 같은 공식이 얻어집니다.

fundamental matrix eq

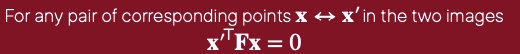
Fundamental Matrix는 아래와 같은 특성이 있습니다.

- image pair에서 F는 유일하다.

- 7자유도를 갖습니다.(scale : -1, det(F)=0 -> singularity->rank2 :-1)

 

Essential Matrix

 다음으로는 Essential Matrix을 보겠습니다. Essential matrix는 단순하게 Fundamental Matrix에서 Intrinsic을 알고 있다는 가정하에 나오는 Matrix입니다. 즉 normal plane상에서 얻어지는 Fundamental Matrix라고 생각해도 됩니다. Intrinsic parameter를 구할 필요가 없으니 계산적으로도 많은 이점을 가지고 있습니다. 

아래는 Essential Matrix를 Fundamental Matrix를 유도한 것과 다른 방법으로 유도해 본 내용입니다.

 

결국 Essential matrix는 t^R의 식으로 구성 되어있습니다. 이 식과 feature의 corresponding pair, 그리고 SVD를 이용하여 최종 Essential Matrix값을 구할 수 있습니다.(두 frame의 relative R|T를 구할 수 있습니다.) SVD의 유도는 추후 기회가 되면 업로드 하겠습니다.

SVD results

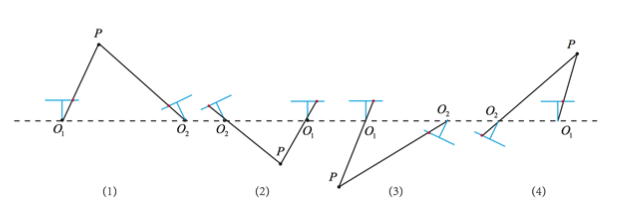
SVD를 이용하여 R|T의 해를 풀면 다음과 같이 4가지의 해가 나옵니다. 이 중 물리적으로 가능한 한가지의 해를 고르게 됩니다.

또한 Essential matrix를 구하기 위한 알고리즘은 8points algorithm과 5points algorithm(Nister, CVPR'03)이 있습니다. 

 Essential Matrix는 몇가지 문제를 가지고 있습니다.

첫쨰로, mono cam의 경우 scale ambiguity가 발생합니다. Essential Matrix를 통해 구한 t에서 만약 [1,0,0] 나왔다면 1m인지 1cm인지는 알 수가 없습니다. 그래서 만약 1m로 정하겠다고 하면 이것을 기준으로 baseline을 고정합니다. 이 작업을 mono slam에서 initialize라고 합니다. 

 두번째로는 pure rotation시 E값을 뽑아낼 수 없습니다. t=0이므로 E또한 0이 되기 때문입니다. 

 

Recap

Epipolar geometry를 SLAM에서 어떤 방식으로 사용하는지 다시 정리하겠습니다.

1. feature extraction (i.e. SIFT, ORB, DL based method ..)

2. matching corresponding

3. loop(RANSAC)

   - sampling paired points (7points for F, 5points for E)

   - F or E 구하기

   - inliers 개수 카운팅

   - threshold 만족 혹은 interation 다 돌았는지 확인

 4. 3번에서 Inliers개수 가장 큰 pairs로 F or E 구하기

---

 

2D-2D geometry관련하여 살펴보았습니다. camera distortion부분과 SVD derivation부분은 추후 추가 할 예정입니다.