[mathematic] SVD, 특이값분해

정의

 우선 특이값(singular value)의 정의부터 보면, 임의의 행렬 A(mxn)의 특이값(singular value)는 $A^{T}A$에 대한 교윳값의 양의 제곱근입니다. 

 SingularValue Decomposition(SVD)는 mxn차원의 행렬A에 대해 위에서 정의한 singular vaule와 singular vector로 decomposition하는 방법을 의미합니다.

식으로 표현하면 아래와 같습니다.

svd definition

orthogonal matrix는 대표적으로 회전행렬을 들 수 있고 아래의 성질을 만족합니다. 

orthogonal matrix

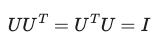
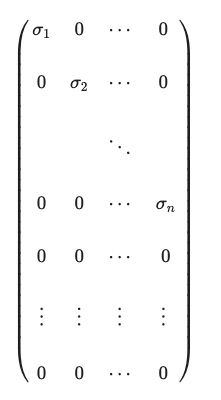
구체적으로 $U, V$는 singular vector가 열벡터로 이루어진 matrix이고, diagonal matrix는 대각성분을 제외한 원소의 값이 모두 0이고,주대각 성분에 A의 singular value를 큰 수부터 차례대로 넣은 행렬입니다. 아래는 그 예시입니다. 보통 최적화 문제에서 overdeterminant 경우가 많아 아래 같은 형태의 diagonal matrix를 많이 보게 됩니다. (m>n인 경우)

diagonal matrix

SVD를 그림으로 도식화하면 아래와 같습니다.

svd . by wiki

아래는 singular value를 구하는 예제입니다.

example1

---

기하하적 의미

svd 기하하적의미

행렬 A를 이용하여 임의의 점(혹은 벡터)를 선형변환한다고 가정하면, [ $ f(x)=Ax $ ]

orthogonal matrix($U , V $)는 회전변환에 대당하고, $\sum$는 각 기저벡터(축방향)으로의 확대 혹은 축소변환을 나타냅니다.

 

---

SVD 정리 및 예제

아래 그림은 지금까지 설명한 것을 정리한 내용입니다.

overview of SVD

다음으로 SVD를 직접 구해보는 예제입니다.

example2

---

응용분야

 

데이터 압축

rank가 r인 행렬A를 k(k<r)의 특잇값만 고려하여 나타내 표현하는 것을 low rank approximation이라고 합니다. 아래의 음영 표시된 부분을 고려하지 않게 됩니다.

low rank approximation

이는 영향력이 큰 k개의 특이값만 고려하여 저장한다는 의미가 되며 저장 공간을 절약할 수 있습니다.

예를 들어 resolution이 600x465인 사진을 rank 1까지 근사한다고 하면, 저장되는 성분은 $U(465\times 1)+ \sum(1) + V(465)$으로 279000에서 1066으로 압축됩니다.

 

pseudo-inverse

우리말로 의사 역행렬이라고하는데, squre matrix가 아닌 행렬에 대해 역행렬의 역할을 합니다.

$A = U \sum V^{T}$로 표현할 때, pseudo inverse는 $A^{+} = V\sum^{+}U^{T}$로 정의합니다. $\sum^{+} = diag(\frac{1}{\sigma_{1}},\cdots ,\frac{1}{\sigma_{r}},0,\cdots,0)$

 

최소제곱해

Homography

이상으로 SVD포스팅 마칩니다.