[SLAM] 2.리군, 리대수(Lie Group, Lie Algebra)

728x90

안녕하세요. 후니대디입니다.

Lie Group, Lie Algebra에 대해서 포스팅하겠습니다.

Lie라는 이름이 지어진 이유는 Lie Group에 대한 이론을 정립한 수학자 이름이 Sophus Lie이기 때문입니다. 리군,리대수는 사실 이해하기 굉장히 난해합니다. 최대한 핵심만 추려서 적어보겠습니다.

정 의

리군(Lie Group)은 discrete하지 않은, 즉 continuous한 그룹이면서 smooth manifold인 집합을 말합니다. smooth와 continuous라는 단어에서 알 수 있다시피 미분가능한 그룹입니다. 예를 들면 좌표변환이 time domain상에서 연속적으로 발생한다고 하면 해당 좌표의 평면상의 한점은 연속적으로 변하게 됩니다. 갑자기 사라졌다가 나타나지 않고 smooth한 움직임을 나타내죠. 이런 연속적인 변환은 리군에 포함됩니다.

리군은 smooth manifold위의 항등원(identity element)위의 접평면(tangent space)에서의 원소와 대응되는 관계를 가지고, 대응되는 이 접평면이 리대수 Lie Algebra를 뜻합니다. 정리하면 Lie Group에 속한 smooth manifold에서의 특정한 원소에서 convolution연산을 통하면 Lie Algebra로 매핑될 수 있습니다.(1:1 매핑)

두개념의 관계가 중요한 이유는 smooth manifold상에서 어떠한 문제를 풀기 복잡한 경우 Lie Algebra로 매핑시켜서 계산을 하게 되면 접평면 위에 있기 때문에 linear한 system상에서 문제는 푸는 것과 동일하게 되어 쉽게 풀 수 있습니다. 즉, linear vector space(Lie Algebra)에서 연산을 수행한 다음 다시 이를 manifold상으로 변환합니다. 변환하는 convolution 연산은 뒤에서 설명할 Exponential Mapping, Logarithm Mapping입니다.

*참고 : manifold라함은 manifold내부에 있는 임의의 점에 대해 Euclidean 구조를 갖는 기하학적 공간이라고 하는데, 풀어 설명하면 군(Group)이 가지는 constraint space를 의미합니다. 즉, 군에 속해 있는 원소들이 constraint내에서 표현가능한 euclidean의 영역입니다.

SO3

Lie Group(smooth manifold)중에 하나인 Special Orthogonal 3 - SO3(대문자)는 3차원 Rotation Matrix와 이에 닫혀있는 연산들로 구성된 군입니다.

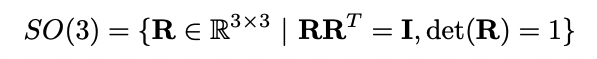
so3

so3(소문자)는 SO3군의 Lie Algebra(접평면)입니다. skew symmetric matrix로 아래와 같이 정의합니다.

SO3 Exponential Mapping

제일 처음 Lie Group, Lie Algebra 정의에서보면 Lie Algebra(접평면)에서 Exponential Mapping을 통해 Lie Group(smooth manifold)으로 변환할 수 있다고 말씀드렸습니다. 아래는 이를 증명한 내용입니다.

Exponential Mapping으로 Lie Algebra에서 Lie Group 매핑되는 것은 위에서 보였습니다. 다음으로 그럼 이 exponential 을 어떻게 계산하는지 보겠습니다.

SO3로 Exponential map을 계산하였더니 이전 포스팅에서 다룬 Rodrigues 공식이 나왔습니다.

[SLAM] 1. 3D Rigid Body Transformation, 좌표계 변환

안녕하세요. 후니대디입니다. 이번에는 3D 좌표계와 좌표계 변환에 대해서 포스팅하겠습니다. Fixd RPY axis angle 3차원 공간을 기준으로 알아보기 전에 쉽게 2차원 공간부터 살펴보죠. 위의 그림은 x

jaehoon-daddy.tistory.com

즉, 로드리게스도 Lie Algebra에서 Lie Group으로 매핑시키는 연산중의 하나라는 뜻입니다. Lie Group 이론이 더 큰 범주라고 할 수 있죠.

SO3 Logarithm

Logarithm은 반대로 Lie Group에서 Lie Algebra로 매핑시키는 연산입니다. 보통 잘 쓰이지는 않습니다. 공식은 아래와 같습니다.

Recap

정리하면 우리가 보통 생각하는 3차원 유클리드 공간에서 움직임을 표현한다고 할때 하나의 질점, rigid body라고 가정하면 움직임은 smooth manifold상에 닫혀있습니다. 하지만 기존의 rotation matrix로 표현하기에는 많은 contraint때문에 최적화 등에 문제가 생기에 되는데 이때 Lie algebra에서 연산을 수행하고 exponential mapping을 통해 이에 대응되는 Lie group,즉 우리가 표현하는 rotation matrix로 결과를 받아온다고 생각하면 됩니다.

SE3

Lie Group 중 하나인 Special Euclidean 3 - SE3(대문자)는 3차원 공간 상에서 강체의 변환과 관련된 행렬과 이에 닫혀있는 연산으로 구성된 Group입니다. 아래에서 R은 SO3에 속하는 3X3행렬이고 t은 3차원 벡터입니다. 이전의 포스팅한 Homogeneous Transform과 형식이 같습니다.

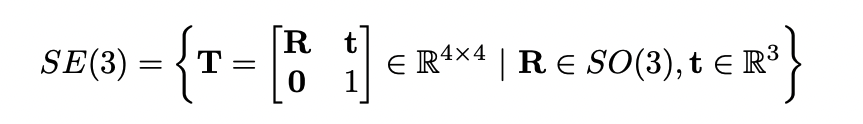
SE3의 임의의 행렬의 역행렬은 다음과 같습니다. 증명은 풀어 계산해보면 간단합니다.

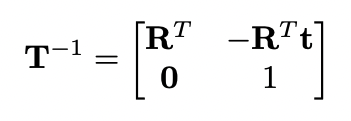
se3

SE3군의 Lie Algebra인 se3는 4X4행렬 혹은 6차원 벡터로 정의합니다. w(3차원벡터)는 각속도를 의미하고 v(3차원벡터)는 linear 속도를 의미합니다. w,v는 순서가 바뀌어 쓰기도 합니다.

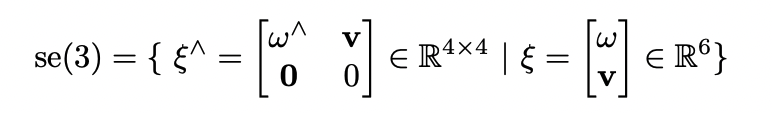
SE3 Exponential Mapping

rotation부분은 so3와 동일하고 translation부분이 추가되었습니다. 자세한 유도는 아래와 같습니다.

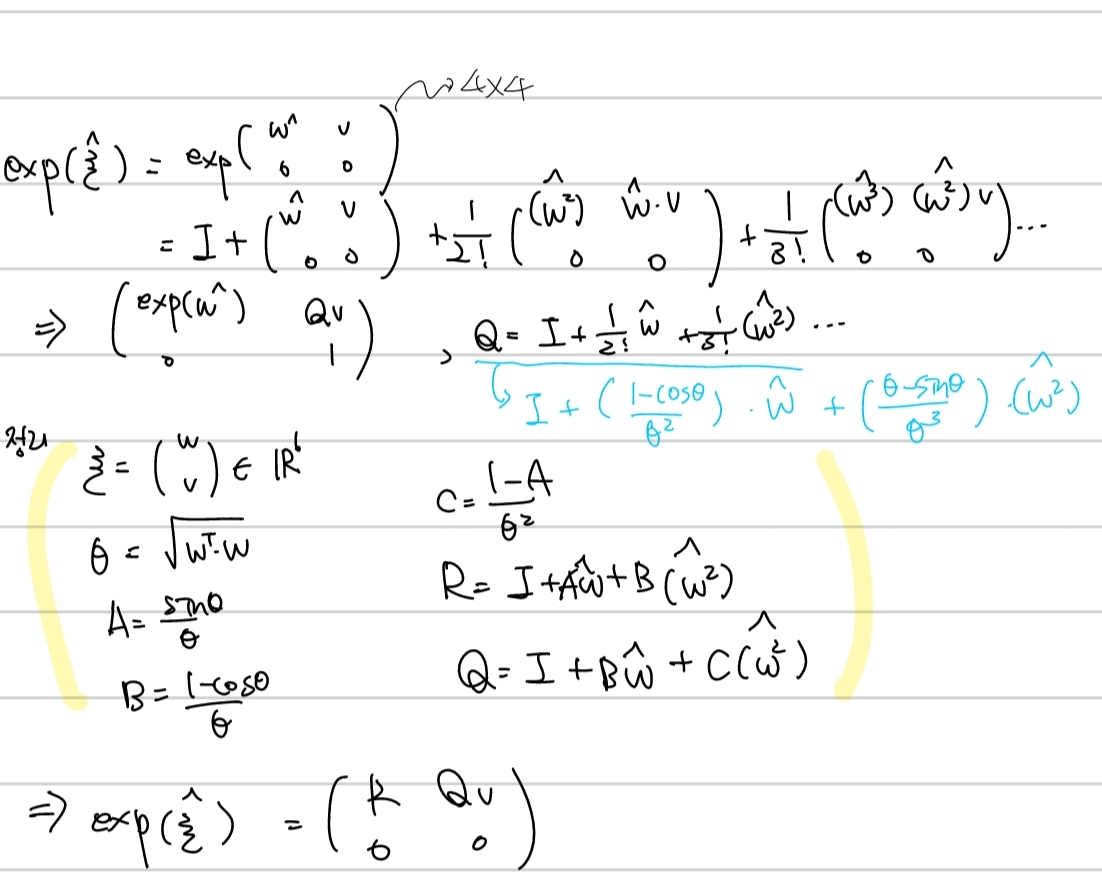
SE3 Logarithm

se3의 Logarithm 연산도 마찬가지로 Rotation 부분은 so3의 Logarith연산과 동일합니다. translation부분 연산만 추가되었습니다.

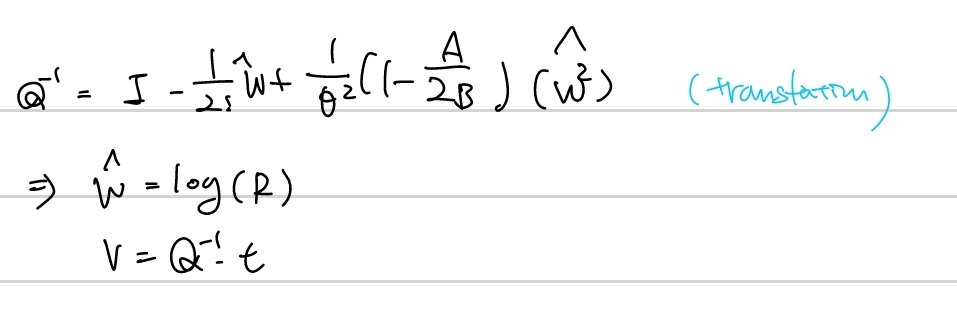
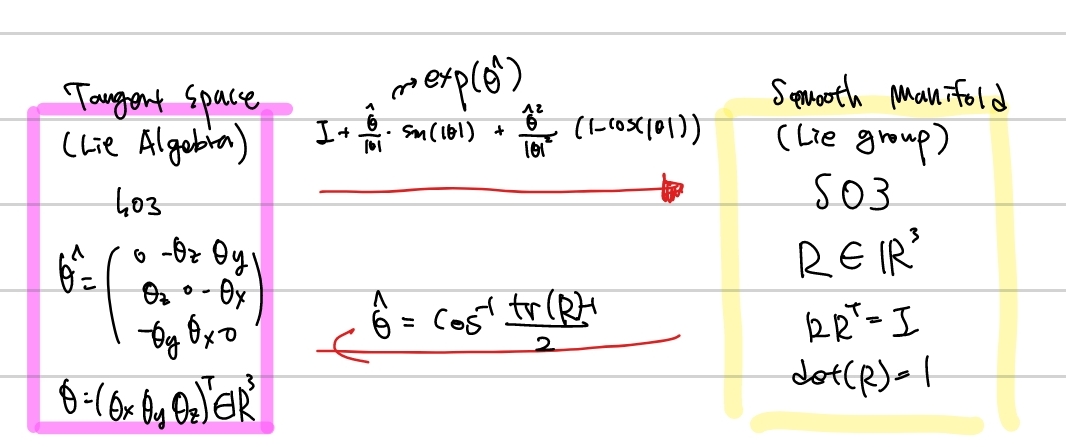
Recap2

지금까지 이야기한 부분을 도식화하였습니다.

SE3 > SO3 > Rodrigues > Euler

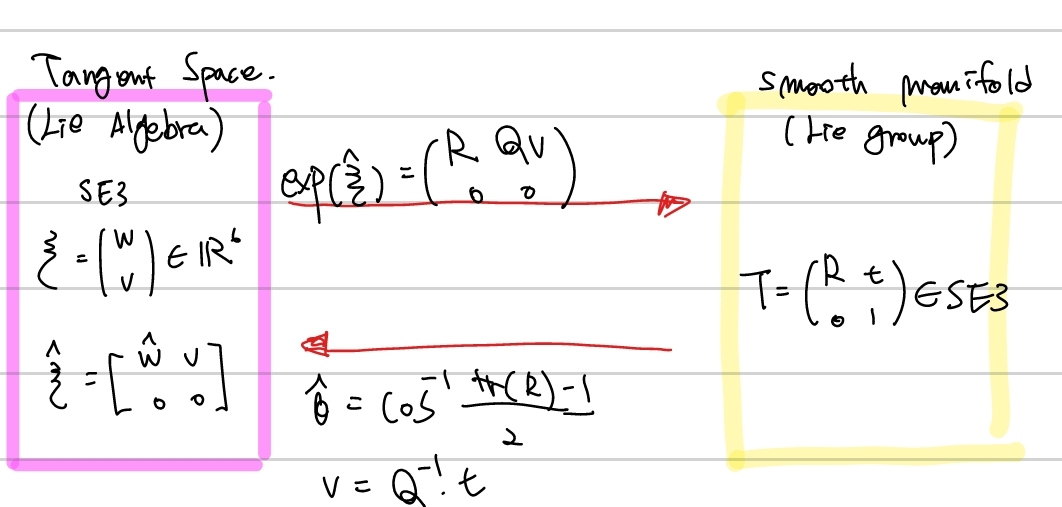
conclusion

결론은 이렇게 어려운 개념의 회전변환 방법을 왜 사용하는지를 다시 말씀드리고 마치겠습니다.

SE3에서 회전 및 이동변환을 구할때 한두번 계산할때는 큰 문제가 없습니다. 하지만 SLAM에서와 같이 매우 빠른시간에 연속적으로 R|T를 변수로 하여 pose를 최적화를 통해 구하는 경우에, SE3상에서는 constraints로 인해 최적화 할때마다 이 조건들이 맞는지 확인해야 합니다. 하지만 se3에서는 이런 constraints가 없고 linear space이기 때문에 부담없이 미분을 적용하여 최적화를 수행할 수 없습니다. 즉, 최적화 변수를 se3(w,v)로 놓고 계산된 증분량을 exp(zeta)를 통해 SE3로 변환하면 됩니다. constrained optimization이 unconstrained optimization으로 변환되는거죠.

또한 최근에 learning based SLAM같은 경우 뉴럴넷에서 R|T를 편미분해야하니 Lie pytorch를 이용하여 Lie group을 활용합니다.

아래 SO3, SE3를 비교한 표를 끝으로 마치겠습니다.

이번 포스팅 내용은 아래 Daniel cremers 교수님의 강의자료와 강의영상, visual slam tutorial pdf를 참조하였습니다.

저작자표시 비영리 변경금지

정 의

SO3

so3