[SLAM] 5. Optimization, 비선형 최적화

이번 SLAM tutorial 에서는 최적화 관련하여 포스팅하겠습니다.
최적화(혹은 수치해석)은 SLAM에서 backend부분에 쓰이는데, MAP point를 이용하여 optimization 후 odometry의 accuracy를 높이는데 보통 활용됩니다.
조금 더 구체적으로 센서 및 real world에서는 noise가 존재하는데 이 때문에 camera 센서를 통해 얻은 이미지로 odometry를 구하더라도 정확한 GT값을 얻기는 힘듭니다. visual SLAM에서는 camera가 여러 시퀀스에서 이미지를 얻습니다. 그 과정에서 한 지점을 여러 번 관찰하게 되고 이를 최적화를 사용하여 노이즈를 최소화하게 됩니다.

---

Optimization

위키피디아의 정의를 보면 optimization이란 집합 위에서 정의된 살수값, 함수, 정수에 대해 그 값이 최대나 최소가 되는 상태를 해석하는 문제라고 정의합니다. 즉, objective function을 최대화(cost function의 최소화)시키는 파라미터를 찾는 문제를 뜻합니다.
또한 최적화를 분류해보면 아래와 같습니다.

최적화

 

Principal

최적화의 원리를 간단합니다. Object Funtion을 보고 (cost function이라고 합시다) function value가 가장 작게 하는 지점을 찾는 것입니다. 그 과정은 임의의 지점에서 내리막인지 오르막인지 보고 내리막인곳으로 조금씩 내려갑니다. (물론 local minimum에 빠질수 있습니다.)

optimization graph

여기서 어느 방뱡으로 얼만큼 이동할 건지에 따라 최적화의 기법들이 나눠지게 됩니다.

Gradient Descent

gradient descent

1차 미분을 통한 최적화 방법의 대표로 gradient descent를 들 수 있습니다. 딥러닝에서 대표적인 최적화 방법으로 일반적으로 느리게 찾을 수 있지만 local minimum에 빠질 확률이 적다고 알려져 있습니다.
$x \subset R, x_{k+1} = x_{k} - \lambda f^{'}(x_k)$다변수함수에서는 $x_{k+1} = x_{k} - \bigtriangledown f(x_k)$ 으로 표현 할 수 있는데 임의의 지점부터 수렴할때 까지 반복합니다. 얼마나 이동할지의 $\lambda$는 하이퍼파라미터로 보통 개발자가 튜닝을 하죠.

step size

$\lambda$의 크게에 따라 수렴속도가 달라집니다. 보통 클 수록 수렴이 빨리지나 잘 못하면 위의 그림처럼 발산의 위험이 있습니다.

Newton' method

newton method

앞서서 일차미분의 문제를 해결하기 위해 이차미분을 이용한 방법들이 생겨났습니다.
$x \subset R, x_{k+1} = x_{k} - \frac{f^{'}(x_k)}{f^{''}(x_k)}$ 다변수함수에서는 $x_{k+1} = x_{k} - H_f(X_k)^{-1} \bigtriangledown f(x_k)$

뉴턴법

이차미분을 통해 최적화를 진행할 경우 일차미분을 통해 진행할때 보다 빠른 수렴과 하이퍼 파라미터 람다를 요구하지 않는 장점이 있습니다. 이차미분이 step을 결정해주기 때문이죠.
하지만 이 또한 문제를 갖고 있는데 변곡점에서 매우 불안정한 특성을 보인다는 점입니다. 즉 위의 식에서 분모인 $f^{''}(x_k)$를 0으로 만드는 부근에서 발산할 우려가 있죠. 두번째의 문제는 극대 극소를 구분하지 못하는 점입니다.
참고로 위의 그림은 일차미분한 f의 해를 구하는 것입니다. 이는 즉 f의 최대 최소를 구하는 것과 동일합니다. 반대로 말하면 f의 최대 최소가 아닌 방정식의 해를 구하는 equation에서는 newton법을 1차 미분을 이용하여 구할 수 있겠습니다.(즉, f=0의 해를 구할떄는 1차미분만으로 가능합니다)

최소제곱법(Least Square Method)

이쯤에서 최소제곱법에 대해서 다루고 가겠습니다. 최소제곱법은 residual의 제곱의 합을 최소화하는 변수를 구하는 방법입니다. 즉, 시스템 모델을 만들고 모델을 통해서 나온 결과값과 데이터값의 차이(residual)를 최소화 시키는 파라미터를 구하는 방법입니다.

최소제곱법

이를 구하는 방법은 수치해석방법 혹은 Linear Algebra를 이용하는 방법이 있습니다.
선형대수를 이용하는 방법은 아래와 같습니다.

Linear Algebra

[mathematic] SVD, 특이값분해

유사 역행렬 (Pseudo Inverse Matrix)

수치해석을 이용하는 방법으로는 최소제곱법을 이용한 다양한 방법들이 있습니다.( 아래 설명할 예정입니다.)
최소제곱법은 결국 $y-(system equation) =0 $의 해를 구하는 것과 동일하다고 볼 수 있습니다. 어쨌든 모델에서 나온값과 GT값의 차이를 최소화 시키는 파라미터를 구하는 것이니 최적화의 한 범주라고 할 수 있겠습니다.

Gauss-Newton method

첫번째로 가우스 뉴턴법입니다. 위에서 뉴턴법이 해를 구하는 방법에서도 사용된다고 말씀드렸습니다.(사실 해를 구하는데 더 많이 쓰입니다.) 뉴턴법에서 해를 구하는 방법을 연립방정식으로 확장한 것이 가우스 뉴턴법이라고 보시면 됩니다. 최적화란 집합 혹은 함수에서 최적값을 구하는 것인데 최소제곱법을 이용하면 0이 되는 곳이 최적값이므로 이를 위해 최소제곱법 equation의 해를 구하는 방법으로 가우스 뉴턴법을 사용한다고 이해하시면 되겠습니다.

가우스뉴턴법

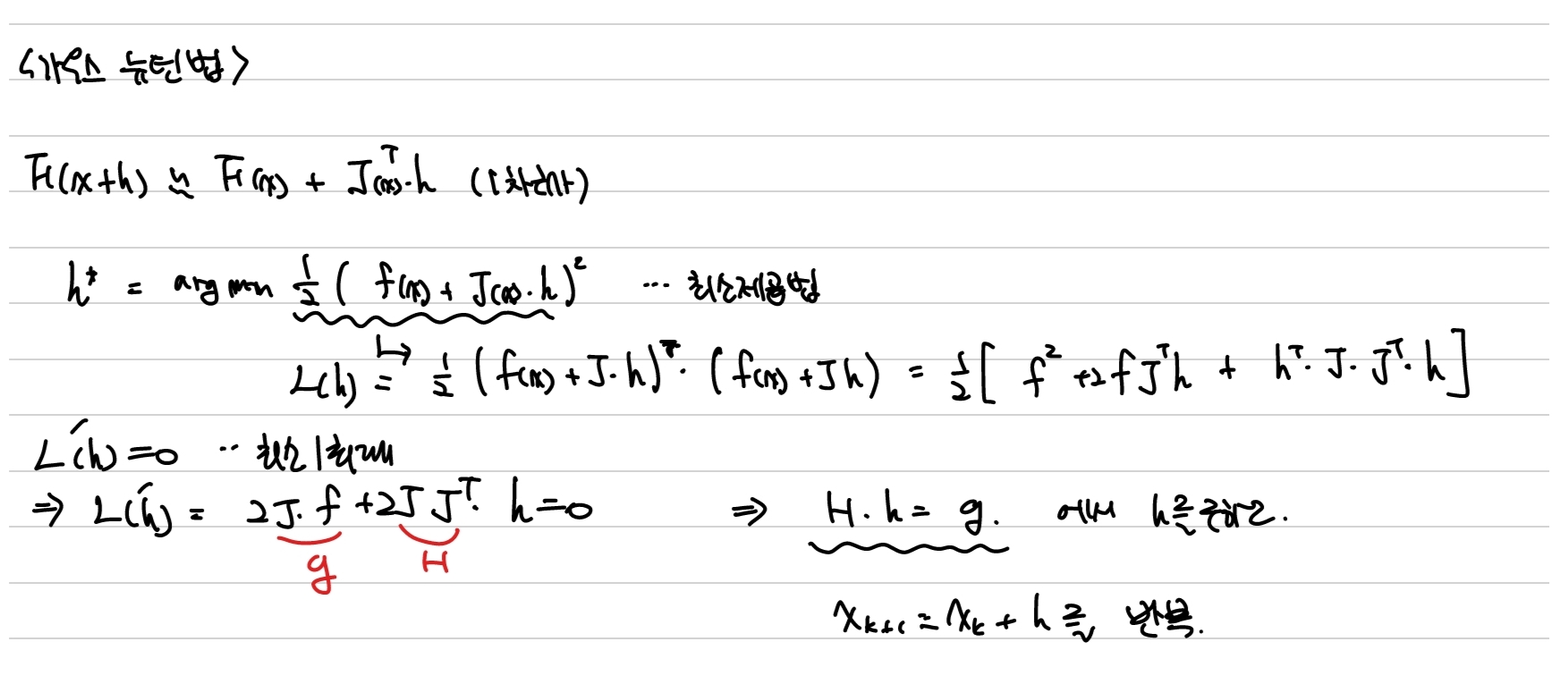
여기서 $JJ^{T}$는 뉴턴법의 헤시안과 비교할 수 있습니다. 자코비안을 구한 후 위의 식을 통해서 iterative하게 적용하면 원하는 모델 방정식을 구할 수 있습니다. 수치해석을 적용한 것들은 선형대수학을 이용한 것과는 다르게 iteration이 동반됩니다.

Levenberg-Marquardt

LM

줄여서 LM방법은 가우스 뉴턴법과 gradient descent방법이 결합된 형태입니다. 해가 멀리 있을때는 gd방식으로 해 근처에서는 가우스 뉴턴방식으로 해를 찾습니다. 많은 최적화 문제에서 LM방법이 사용됩니다.
Levenberg-Marquardt방법은 기존의 Levenberg방법을 개선시켰는데  Levenberg방법을 살펴보면 가우스 뉴턴법을 개선하여 H항에 $\mu $항을 더함으로써 발산의 위험성을 낮춥니다.  $\mu $을 damping factor라고 하고 값이 작으면 가우스 뉴턴법과 비슷하고 값이 크면 gradient descent 방법과 유사해집니다. 그렇기 때문에 iteration을 돌면서 안정적으로 해에 수렴할 경우 작은값을 주고 그렇지 않은경우 큰 값을 줍니다. 즉 값이 adaptive합니다.
여기서 더 나아가 Levenberg-Marquardt방법은 항등행렬 I대신에 $diag(J^{T}J)$를 더해주는 방식을 제안합니다. $diag(J^{T}J)$은 파라미터 성분에 대한 곡률을 나타내기에 singular문제를 비하면서도 곡률을 반영할 수 있습니다

---

이상으로 최적화편 포스팅 마치겠습니다.