![[SLAM] 6. Bundle Adjustment](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FV8kRq%2Fbtr9rhEW5SJ%2Fx64WUKa4t45z3vudAc8gZK%2Fimg.png)
이번 SLAM tutorial 에서는 BundleAdjustment에 대해 포스팅하겠습니다.
앞서 5번째 SLAM tutorial 포스팅에서는 nonlinear optimization에 대해서 설명하였습니다. BA(Bundle Adjustment)는 nonlinear optimization을 사용하는 대표적인 application입니다.
Intro
우선 bundle adjustment를 언제 왜 사용하는지부터 살펴보겠습니다. 이를 위해 앞장에서 설명한 것들을 다시 overview해보겠습니다. mono-cam의 경우라하면, 연속된 이미지 두장을 통해 initialization을 합니다. 이 과정에서 Essential Matrix 혹은 Fundamental Matrix를 통해 두 image사이의 R|T 즉, geometrical한 관계를 알 수 있습니다.
[SLAM] 3. 2D-2D geometry, Epipolar Geometry
안녕하세요. 후니대디입니다. 이번 포스팅은 2D-2D (two view) camera geometry에 대해서 살펴보겠습니다. Camera Model 시작하기전에 camera model 먼저 살펴보겠습니다. 3D world의 points를 2D image plane에 매핑하는
jaehoon-daddy.tistory.com
두 이미지 사이의 관계를 알게되었으니 이제 Triangulation 등의 3D-2D geometry를 통해 3D points를 얻을 수 있습니다. 이렇게 얻은 3D point(map point)와 다음 image와의 관계를 통하여 다시 R|T를 구할 수 있습니다.(PnP solver)
[SLAM] 4. 3D-2D geometry, Triangulation, PnP
안녕하세요. 후니대디입니다. 지난번에는 2D-2D geometry로 Essential Matrix, Fundamental Matrix에 관해 다루어봤습니다. 즉, Two view가 존재할때 (stereo 혹은 sequenced frame) two view간의 관계를 설명해보았습니다.
jaehoon-daddy.tistory.com
여기까지가 보통 SLAM에서 이야기하는 Front-end부분이 되겠습니다. 혹은 tracking이라고 할 수도 있습니다. Front-end에서 여러 테크닉을 통해 noise를 제거하여 pose estimation을 하였다고 하더라도, 오차는 발생할 수 있고 이렇게 쌓인 drift error는 시간이 지나면 걷잡을 수 없게 커지게 됩니다.
이를 막기 위한 장치가 SLAM에서 Back-end부분에서 할 일이고 대표적으로 Bundle Adjustment의 역할입니다.
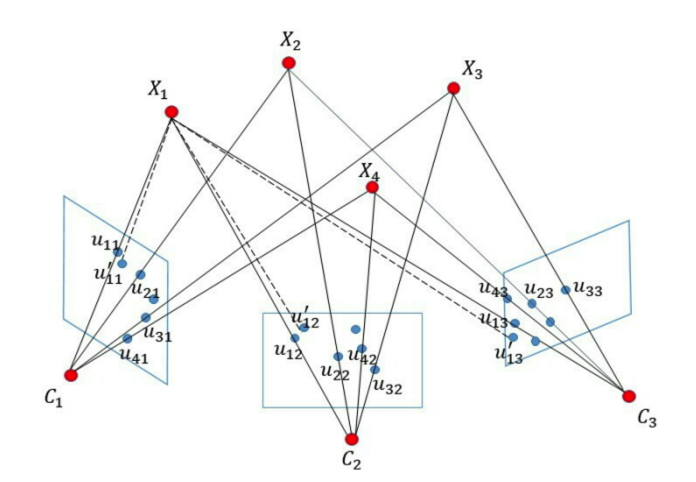
방법은 위의 그림을 보며 설명하겠습니다. 간단한 예를 들면, $C1$,$C2$ 두 장의 이미지에서 $u_{xx}$는 feature point입니다. 이 points와 Essential matrix, Triangulation, PnP를 이용하여 3D의 map point $X_{x}$를 구합니다. 이렇게 구한 3D map point를 다시 $C_{2}$ 혹은 $C_{3}$ 2D평면에 projection합니다(re-projection). 이 점이 $u^{'}_{12}$, $u^{'}_{13}$이 됩니다. 그럼 projection한 point($u^{'}_{12}$, $u^{'}_{13}$)와 그것에 대응되는 실제 feature point( $u_{12}$, $u_{13}$) 차이를 최소화 하도록 map point를 numetrical 방법으로 refinement하게 됩니다. 여기서 사용되는 numerical 방법은 이전에 포스팅했던 non-linear optimization이 되겠습니다.
[SLAM] 5. Optimization, 비선형 최적화
이번 SLAM tutorial 에서는 최적화 관련하여 포스팅하겠습니다. 최적화(혹은 수치해석)은 SLAM에서 backend부분에 쓰이는데, MAP point를 이용하여 optimization 후 odometry의 accuracy를 높이는데 보통 활용됩니
jaehoon-daddy.tistory.com
Bundle Adjustment
1. Cost Function
BA의 cost function으로는 reprojection error를 사용합니다. reprojection error를 이해하기 위해 camera의 projection 과정을 전체적으로 살펴보겠습니다.
위의 그림은 3D 공간의 map point에서 2D image plane으로 projection하는 과정을 순서대로 나열한 것 입니다.
1단계에서는 world coordinate에서 camera coordinate으로 R,t 매개 변수를 활용하여 변환하는 식입니다.
2단계에서 변환된 3D point를 normal plane에 projection합니다.
3단계에서는 distortion을 고려합니다.
4단계에서 마지막으로 camera intrinsic parameter를 기반으로 pixel (u,v)를 계산합니다.
$z-h(\xi,p)$에서 z는 image상에서 측정된 3D point의 pixel 값입니다. h함수는 위에서 설명한 projection단계를 뜻하고 변수 $/xi$는 camera pose인 R,t를 $p$는 3D point를 의미합니다. 즉, $z-h(\xi,p)$라는 cost function 혹은 reprojection error를 최소화 하는 R,t, 3D point를 구하는 것이 Bundle Adjustment(BA)의 목적입니다.
2. BA방법
1에서 정의한 cost function을 가지고 어떻게 BA를 하는지 보겠습니다.
우리는 cost function으로 정의한 reprojection error를 최소화하는 parameter(R,t,3D points)를 찾는 것이 목적이고 non-linear한 모델이기 때문에 non-linear least square에 정의에 의해 위의 그림처럼 나타낼 수 있습니다. 여기서 $\Delta x$를 구하여 incremental하게 최적의 parameter를 구하게 됩니다. 자세한 내용의 위의 삽입한 chap 5의 optimization편을 참고해주세요.
요약하면 talyor 정리에 의해 $e(x)+J\Delta x$로 approximation할 수 있고 이를 newton method를 이용하여 $H\Delta x=-b$로 정리되 $\Delta x$를 구할 수 있습니다.
위의 그림은 앞서 설명한 일반적인 newton method를 BA에 맞게 식을 세운 내용입니다.
결국 최적의 camera pose(R,t)와 3D points(p)의 값을 찾는 것을 목적으로 최적화 식을 세웠고, newton method 정리에 의해 나온 $H\Delta x=g$에서 $H$를 computing issue없이 구하는 것이 다음 목표가 되겠습니다.
3. Hessian 잘 구하기
다음 목표인 computing issue를 해결하는 것이 가장 핵심은 H(Hessian matrix)를 잘(?) 구하는 것입니다.
global optimization을 하게 되면 수많은 landmark와 camera pose를 최적화해야하기 때문에 matrix의 크기가 커질 수 밖에 없습니다. 이를 어떻게 풀어내는지는 아래 그림에서 설명하였습니다.
$H$을 구하기 위한 첫번째 단계는 $J$자코비안을 먼저 구하는 것입니다. 변수로 R,t,P(points)로 설정하였기 때문에 이를 변수로한 1차 편미분이 $J$이 되겠습니다. 구한 J를 이용하여 H를 구하게 되면 sparse matrix 형태를 띠게 됩니다. 많은 부분이 0으로 채워진 block matrix의 형태를 갖습니다.
최종적인 식 $H\Delta x=g$에 H를 대입하여 $\Delta x$를 구하기 위해서는 H의 inverse matrix를 구해야하는데 단순히 inverse matrix를 구하게 되면 large scale의 경우 computation issue문제가 발생합니다. 그렇게 때문에 sparse matrix의 특성을 이용하여 schur complement를 이용하여 computing issue를 해결합니다.
위의 그림은 schur complement를 이용하여 $H\Delta x=g$식을 정리한 것입니다. Forward substitution과정에서 marginalized out되서 $\Delta x_p$는 소멸되어 $\Delta x_c$를 구할 수 있게 되고, Backward substitution에서는 구한 $\Delta x_c$값을 토대로 $\Delta x_c$값을 구할 수 있게 됩니다.
Forward substitution에서 최종 $\Delta x_c$구하는 과정에서는 $Ax=B$형태이기 때문에 LU decompostion, cholesky decomposition등의 선형대수 스킬이 사용됩니다.
Robust Cost Function
cost function이 매우 커지게 되면(miss matching, outlier) e값이 지나치게 커질 수 있기 때문에 robust kernel을 이용해 이를 해결합니다.
종류로는 cauchy, huber등 다양한 커널이 존재하며 일반적으로 e가 지나치게 커지는 부분의 기울기를 줄여주는 방향으로 모델링됩니다.
참고) 아래는 BA가 포함된 훌륭한 ETH의 강의자료입니다. BA를 이해하는데 많은 도움이 되었습니다.
이상입니다. 감사합니다
