[paper review] BARF : Bundle-Adjusting Neural Radiance Fields 논문 리뷰

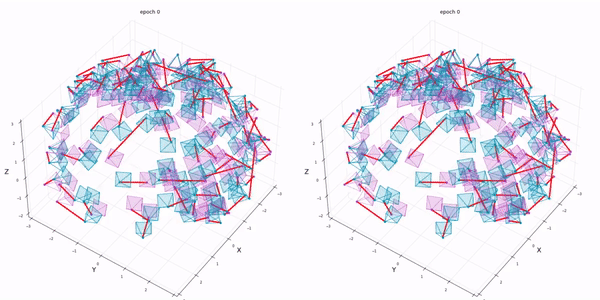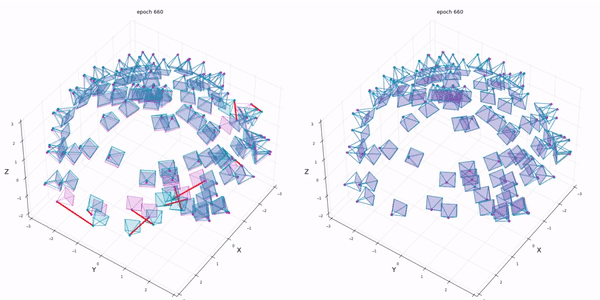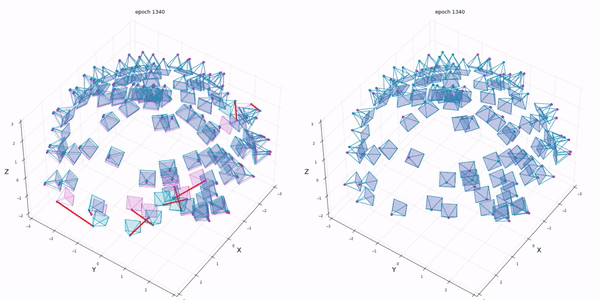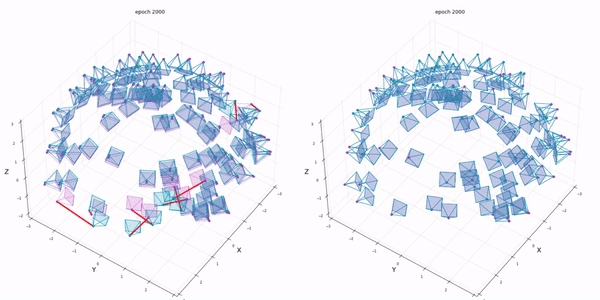
안녕하세요. 이번 포스트는 BARF라는 NeRF에 BA의 아이디어를 접목한 논문을 리뷰하겠습니다.

시작하기 전에 BA, NeRF에 대해서 사전 지식이 필요하기 때문에 아래의 포스트 참고하세요.

[paper review] NeRF 논문 리뷰

[SLAM] 6. Bundle Adjustment

---

Limitation of Vanilla NeRF

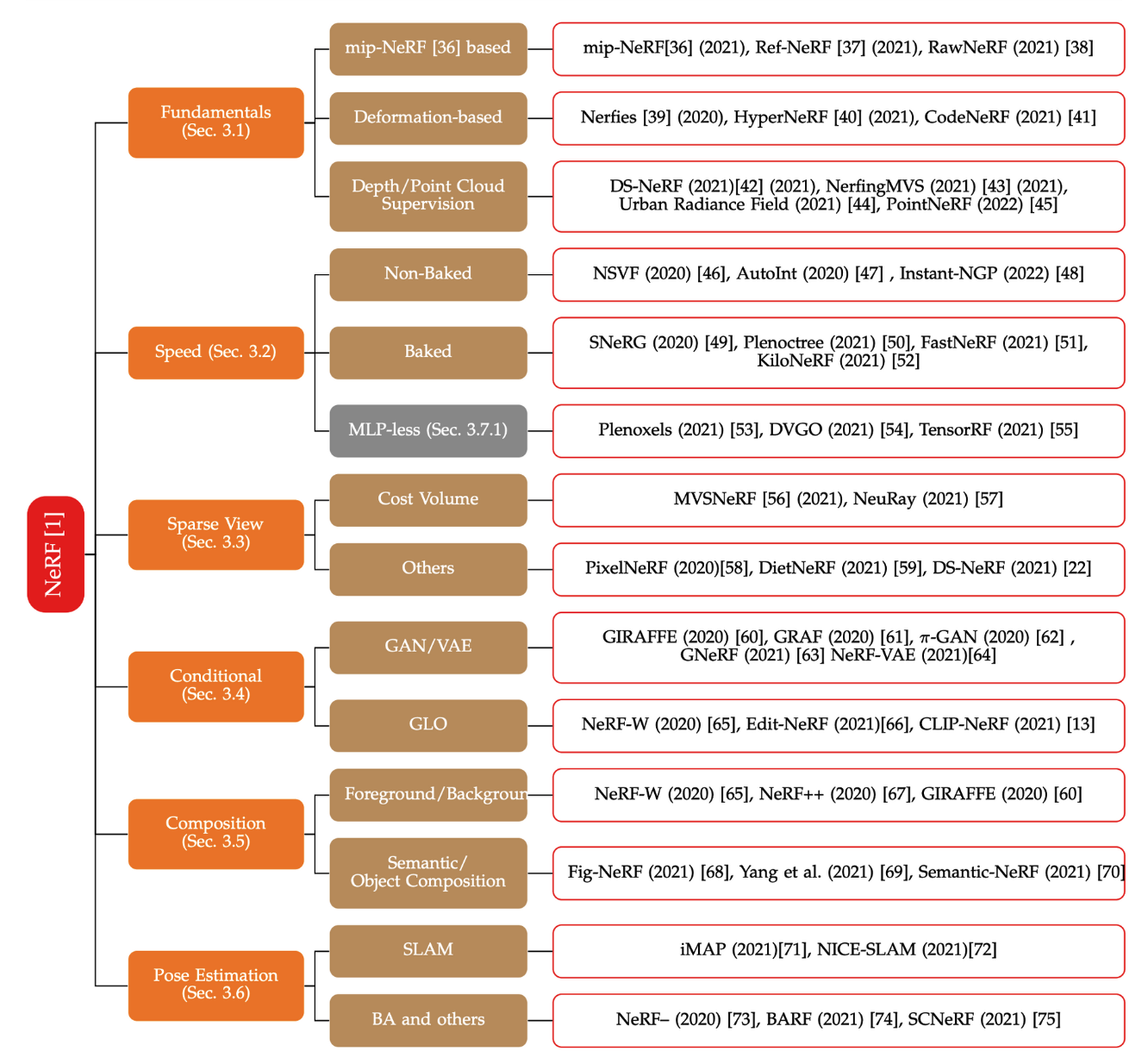
위의 첨부한 그림처럼 NeRF가 publish된 이후에 NeRF의 약점을 보완하는 수많은 파생 NeRF들이 쏟아져 나오고 있습니다. 오늘 소개하는 BARF는 NeRF 모델을 돌리기 위한 꽤 정확한 camera pose가 필요하다는 것을 파고 들었습니다. 부정확한 camera pose가 input으로 들어와도 훌륭하게 representation을 하는 것을 목표로 하고 있고 이를 위해 Bundle-Adjustment(BA)방법론을 이용하여 pose update를 진행합니다. 즉 기존의 NeRF를 통해 representation, BA를 통해 registation을 joint하여 학습하게 됩니다.

---

Planar Image Alignment  2D

논문에서는 컨셉을 소개하기 위해 2D 환경에서를 먼저 예를 들었습니다.

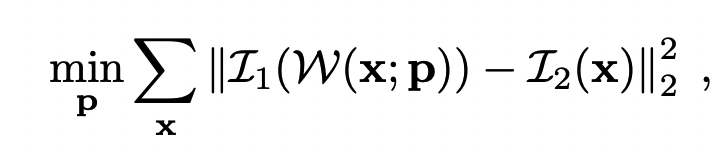
위의 식은 warping parameter를 구하기 위한 cost funtion이라고 볼 수 있습니다. notation을 설명하면 x는 image pixel(u,v), p는 구하고자 하는 warping parameter, I는 image photometric value 이라고 볼 수 있습니다.

즉 Image1에서의 특정 pixel에서 적절한 warpping(구하고자 하는 것)후 점과 image2에서 대응되는 픽셀간의 photometric error를 최소화하는 warpping parameter를 구하는 cost function이 되겠습니다.

warp function은 non-linear이기 때문에 least square(최소자승)으로 최적화 문제를 풀 수 있습니다. SLAM에서는 보통 Gauss-Newton method를 활용하여 문제를 풀게 됩니다.

Gauss-Newton method의 최적화 문제는 보통 위의 그림처럼 정리 됩니다.(자세한건 위에서 첨부한 포스팅 참고)

이에 맞게 cost funtion을 정리한 것이 아래의 식이 되겠습니다.

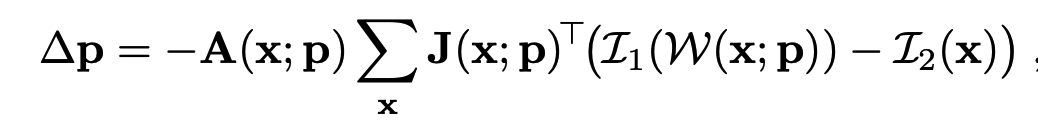
$e$는 residual 값이 되겠고, J(자코비안)은 동일하며 두 식이 다른 점이 있다면 $H$(Hessian), $A$부분입니다. 보통 SLAM에서는 헤시안 matrix의 inverse를 구하기 위해 sparse matrix의 특성을 이용해 schur complement등의 방법을 사용합니다. 하지만 BARF에서는 기존의 representation과 joint하여 learning method로 해당 문제를 풀어야하기 때문에 H를 마치 learning rate으로 스칼라의 하이퍼 파라미터로 정의해서 문제를 풀어버렸습니다. 개인적으로는 위의 최적화 문제를 기존의 nerf method에 녹여서 backpropagation을 통해 학습할 수 있도록 잘 풀어낸것이 이 논문의 contribution이라고 생각합니다.

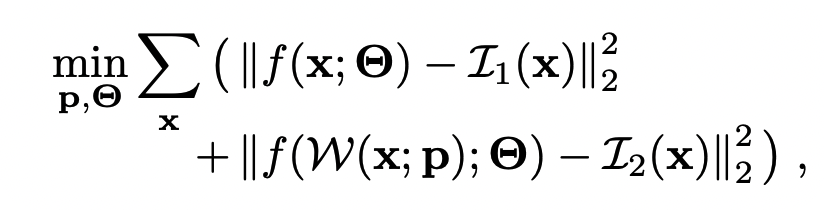
위의 식이 최종 cost function이 되는데 f를 image를 만드는 함수(렌더링하는 함수)라고 가정하고 $ \Theta $는 뉴럴넷은 파라미터, $p$는 camera parameter가 되겠습니다. 그렇게 되면 첫번째 식은 렌더링에 대한 cost function이 될 것이고 두번째 식은 pose refinement에 대한 cost function으로 joint하게 학습이 이뤄지게 됩니다.

---

Neural Radiance Fields 3D

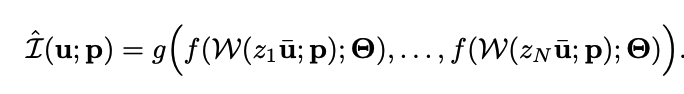
이제 2D에서의 컨셉을 3D로 확장하고 NeRF의 method를 적용시켜 보겠습니다. 2D에서의 f는 $\hat{I}$으로 볼 수 있습니다. 위 식을 풀어 설명해보면 image의 pixel에서 ray를 쏘게 되면 z방향으로 N개의 sampling을 하게 됩니다.(기존의 nerf와 동일) sampling된 3D points ($z_{i}\bar{u}$)를 extrinsic parameter (R,t)$p$를 이용해 Transform($w$)합니다. 이 후에는 f라는 neural network, mlp를 태우고 여기서의 학습해야할 파라미터는 $\Theta$가 되겠습니다. 이 후 나온 값들을 neural redering을 통해 operation하여 해당 위치의 RGB값을 나타내게 됩니다. [Method : Transformation(p) -> MLP($\Theta$) -> neural rendering] 

전체 cost function으로 확대해보겠습니다. M개의 이미지와 target 이미지가 있다고 할때 M개의 이미지의 pixel에서 ray를 쏘도 샘플링 된 points를 P(R,t)를 통해 transformation한 후의 points를 neural rendering 집어넣고 나온 RGB값과 target의 해당 pixel의 RGB값의 차이가 되겠습니다.

위의 loss function(=cost function)을 사용하여 학습하기 위해서는 camera parameter의 경우 앞서 설명했듯이 자코비안을 활용하여 $\Delta p$구해야 합니다. $\Theta$의 경우 기존의 NeRF MLP의 파라미터를 구하듯이 구하면 됩니다.

J는 결국 trasform+MLP+neral rendering의 식을 camera parameter로 편미분하는 것인데 쉽게 구하기 위해 위의 식처럼 체인룰을 사용합니다. 중간에 분모에 x와 분자의 (zu;p)가 다르지 않냐는 의문을 갖을 수도 있는데 이는 같은 것을 말합니다. $\partial W(z_{i}\bar{u}$의 의미가 2D image에 z의 depth를 갖는 point를 transformation한 3D point를 뜻하기 때문에 이는 x를 뜻하여 소거 될 수 있습니다.

 

사실 learning model에 gradient가 아닌 jacobian을 사용하여 backpropagation을 한다는게 낯설긴 하지만 사용한 예시가 있는 방법인 것 같습니다. 사실 어짜피 둘다 일차미분으로 선형근사해서 함수의 극대 극소를 찾는 것이니 가능할 것 같습니다.

Gradient, Jacobian 행렬, Hessian 행렬, Laplacian

Computing the Jacobian matrix of a neural network in Python

 

 

positional encoding

다음으로 positional encoding부분입니다. 기존의 NeRF에서도 position의 augmentation느낌으로 positional encoding을 진행합니다.

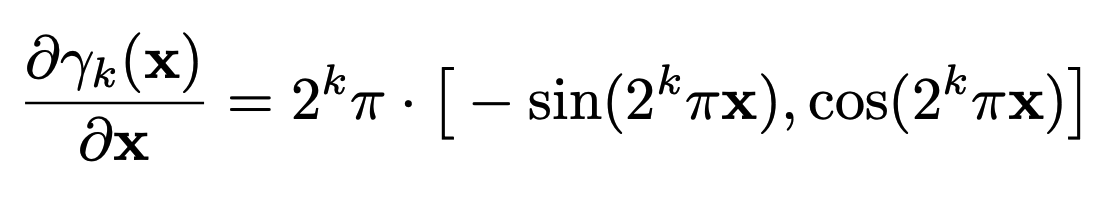
식을 보면 positional encoding의 미분은 signal 증폭이 일어난 상태입니다. 논문에서는 gradient signal끼리의 상쇄현상을 일으키고 gradient signal 일관되지 않은 문제를 지적합니다. signal에 대한 domain지식이 없다보니 해당 부분이 와닿지는 않지만 일단 받아드려면, 그래서 BARF에서는 controllable parameter추가하여 최적화 진행에 비례한 coarse to fine전략을 사용합니다. 즉 registration 먼저 잘 학습이 되면 representation을 고도하는 전략을 뜻한다고 합니다.

---

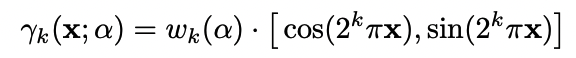
Experiments

실험은 intrinsic parameter는 알고있다고 가정하고 extrinsic parameter에 noise를 추가합니다. BARF는 최소한의 initial guess가 존재해야합니다. 

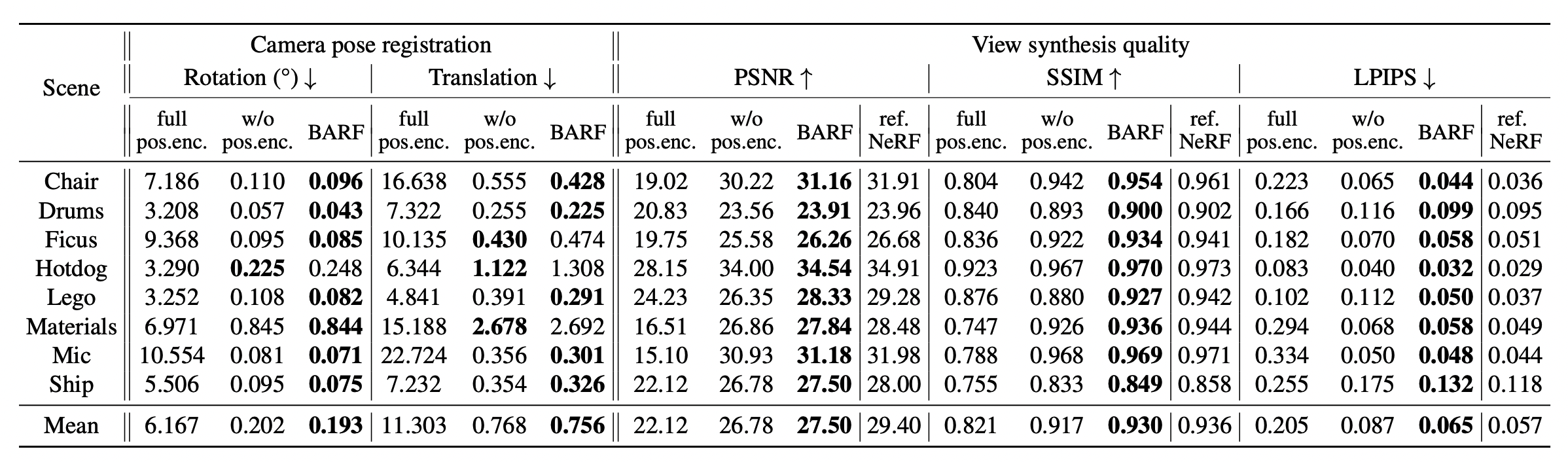
우선 대부분의 실험이 BARF의 positional encoding의 효과에 대해서 언급하고 있습니다.

reference NeRF는 perfect position을 주었을때이고 나머지는 rotation은 최대 14.9도 만큼 translation은 최대 0.26비율만큼 noise를 준 상황입니다.