![[paper review] Loc-NeRF:Monte Carlo Localization using Neural Radiance Fields 리뷰](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbLJEfI%2FbtrPwy1QpLS%2F6vz0IOooMjYCgZFk1d1D4K%2Fimg.png)
안녕하세요. 후니대디입니다.
이번에는 NeRF 시리즈에 연속으로 Loc-NeRF를 리뷰해보겠습니다.
Background
해당 논문은 NeRF를 사용하여 Localization을 시도한 논문으로, 우선 해당 논문을 이해하려면 Particle Filter와 NeRF에 대한 사전지식을 필요로 합니다. 개인적으로는 Loc-NeRF의 novelty는 크지 않지만, localization에 NeRF를 처음 사용해봤다는 것이 의미가 있는 것 같습니다.
NeRF의 사전학습은 이전 포스트로 대체하겠습니다.
[paper review] NeRF 논문 리뷰
최근 synthetic data들의 중요성이 대두되고 있습니다. simulation, generative model 등 여러 방법이 있지만 여기서는 NeRF를 짧게 분석해보겠습니다. 정 의 NeRF는 Novel View Synthesis 계열의 기술입니다. NVS..
jaehoon-daddy.tistory.com
다음으로 Particle Filter에 대해 간략하게 알아보겠습니다. 사실 Filter이론은 Kalman필터부터해서 매우 긴 역사를 가지고 있습니다. SLAM 분야도 이전에는 이 필터기반으로 알고리즘을 만들었고, 많은 상용 이동로봇들이 2D Lidar 센서와 Particle Filter를 이용하고 있습니다.
Kalman Filter는 nonlinear 시스템에서는 사용할 수 없지만, Particle Filter는 nonlinear 시스템에도 적용할 수 있는 장점을 가지고 있습니다. Particle Filter는 Monte Carlo Method를 기반으로 합니다. 해서 본 논문의 제목이 나온 이유입니다. Monte Carlo Method 관련해서는 추후 3D vision을 위한 수학 백그라운드 편으로 기술해볼 예정입니다.
구체적으로 알고리즘을 살펴보면 3단계로 볼 수 있습니다. (4단계라는 제가 임의로 나눈것입니다. 공식적은 아닙니다)
1. Random Sampling
이동로봇의 예를 들겠습니다. 일단 Map정보는 알고있다는 상황입니다.
initial position은 아예 정보가 없기 때문에 랜덤하게 particle를 뿌립니다. 일종의 가상 로봇들이라고 생각하시면 편합니다. 예를 들어 200개의 가상의 로봇들을 맵에 뿌린다고 합시다.
2. Weighted Sampling
로봇이 이동을 하게되면 motion model과 measurement 의 값을 통하여 가상의 로봇들 마다의 weight를 매겨줍니다. 예를 들면 1m를 앞으로 이동했는데 2D 라이다에 [-20rad,20rad] 1m의 벽을 발견했다고 하면 이런 상황에 가상의 로봇들 200개중에 해당상황에 더 가까운 가상의 로봇들에게 더 많은 weight를 줍니다.
3.Resampling
weighted sample 들을 다시 weight가 없는 particle로 바꾸기 위해 resampling을 진행합니다. resampling방법론은 매우 다양하지만, 핵심은 weight가 높은 근처에서 더 많이 parcle을 뽑는것입니다. 보통 Resampling후의 입자의 개수는 그 전과 동일합니다.
1~3의 과정을 반복하면서 파티클들이 어느 지점(가상의 로봇)에 수렴하게 되면서 가장 높은 확률의 위치를 추청합니다. 아래의 그림과 영상을 보시면 좀 더 직관적으로 이해되실겁니다.
Methodology
loc-NeRF의 알고리즘을 살펴보겠습니다. 사실 위에서도 말씀드렸지만 particle filter와 nerf를 알고계시다면 특별할 건 없습니다. 해당 논문에선 4가지 단계로 particle filter를 설명합니다.
0. notation
위의 식은 posterior probability의 식을 뜻합니다. particle filter는 이 posterior probability를 maximization하는 것이 목표입니다.
M은 Map, I는 이미지 value, O는 motion measurement, X는 3차원 pose(R|T)를 뜻하고 이를 풀어 해석해보면 전체의 Map과 time domain에서 시작부터 t까지(현재까지)의 이미지 데이터와 motion measurement 데이터가 주어질때 t에서(현재의) 로봇의(편의상 agent를 로봇이라고 가정) pose가 X일 확률을 의미하며, 이 확률을 maximize하는 X를 찾는 것이 particle filter의 목표라고 정리하면 무리가 없습니다.
또한 위의 posterior를 직접적으로 구하기 현실에서는 어렵습니다. 따라서 베이지안 룰을 이용하여 위와 같이 변경해서 measurement, motion model 을 이용하여 간접적으로 구합니다.
위의 식은 weighted set을 뜻합니다. 즉, 파티클(가상의 로봇들)의 위치와 weight를 set으로 정의합니다.
1. Prediction 단계
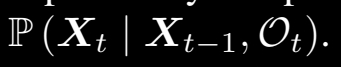
0단계에서 설명드린 motion모델입니다. 즉, 모션 모델을 이용하여 t-1 time step의 결과값을 모션 모델 인풋값으로 하여 t time step의 위치를 prediction합니다. 해당모델에는 system noise가 포함되어있습니다. 본 논문에서는 VIO 혹은robot dynamics(아마 데드레코닉을 뜻하는거 같습니다.) 을 이용하여 motion model을 구성한다고 기술하였습니다.
2. Update 단계
2번째 단계인 update 단계에서 NeRF를 사용합니다. 우선 이 업데이트 단계에서는 measement model을 이용하여 particle에 weight를 주는 단계라고 생각하시면 됩니다. 이 measurement model에 NeRF를 사용하였습니다.
수식으로 살펴보면 위의 measurement model을 이용하여 가상의 로봇들(파티클)에게 weight를 부여합니다. 즉, t시점에서의 위치와 전체 Map을 알고 있을때의 각각 가상의 로봇(파티클)의 이미지값(관측값)이 가지는 확률을 뜻합니다. 어렵게 느껴지실 수 있지만 아래의 수식을 보면 간단합니다.
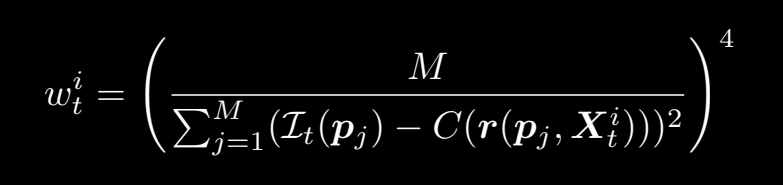
어쨋든 해당 단계에서는 가상의 로봇들의 weight을 구하는 것이 목적입니다. 위의 식을 통해 구할수 있습니다. 풀어 해석해보면 분모는 i번째 가상의 로봇(파티클)에서 찍힌 이미지(measurement)의 intensity와 해당위치에서 Map을 통해 구한 NeRF projection 이미의 intensity의 차이를 뜻합니다. 전체의 pixel을 계산하기에는 computation 문제가 있기때문에 M개의 subset을 구성하였다고 합니다.(randomly pick). 분자는 그 subset 픽셀의 개수입니다. 이 식이 의미하는바는 실제 카메라를 통해 들어온 image intensity와 NeRF를 통해 구한 해당 위치의 projection image intensity의 차이가 작으면 높은 weight를 가져가겠다라는 것을 뜻합니다.
3. Resampling 단계
해당 단계에서는 standard paricle filtering방법과 동일하게 하였다고 합니다. 즉, 제일 처음 설명드렸다시피 weight가 높은 곳 위주로 resampling을 가져갔다고 보시면 됩니다.
4. pose estimate | particle Annealing
해당과정은 computation issue를 막기위해 적용하였다고 기술하였습니다. 아무래도 NeRF자체도 꽤 computation load가 있는데, particle 개수가 많아지면 부담이 될 수 밖에 없습니다. 이를 막기 위해 Annealing기법을 적용하였습니다.
방법은 rule base로 간단합니다. 파티클 필터를 통해 resampling한 파티클들의 spread가 threshhold 보다 작으면 (즉, 일정이상 수렴하면) particle을 random하게 뿌릴때 spread하는 범위를 줄이고, 파티클의 개수 또한 줄여줍니다. 이러한 방식으로 점점 수렴시킵니다.
Experiments
실험은 크게 singe image로 localization하는 것과 tracking하는 것 두개로 이뤄져있습니다.
i) single image
benchmark로는 iNeRF를 사용하였습니다. LLFF dataset을 활용하여 5개의 랜덤 이미지를 선택하여 pose estimation하는 실험입니다. 통제변수로 두 모델다 같은 pre-trained NeRF모델을 사용하였습니다. 결과적으로 위의 plot을 보면 높은 정확도를 나타냅니다. 또한 annealing을 적용하면 더 빨리 satuation되는 것을 보여줍니다.
ii) tracking
tracking experiment입니다. 얼마나 pose를 잘 tracking하는지 실험하는 주제입니다. benchmark로 NeRF-Naviation을 아용하였습니다. 환경은 블렌더로 만든 stonehenge 시뮬레이션 환경을 이용했다고 합니다. NeRF-navigation이 initial value를 알아야하는 알고리즘이라 초기위치는 주어지고 시작하였습니다. plot을 보면 NeRF-Navigation은 image의 개수가 적을 때 렌더링 퀄리티가 낮을 때 강인한 모습을 보이지만 평균적으로 Loc-NeRF의 성능이 우수함을 볼 수 있습니다.
conclusion
해당 논문은 NeRF를 localization에 적용한 최초의 paper인 점에서 의의를 갖습니다. 사실 novelty가 크지는 않지만 application 쪽에서 괜찮은 점수를 받은 것 같습니다. 실험결과에서 기존의 classic한 방법과의 benchmark도 있었으면 좋겠다는 아쉬움이 있습니다. 이를 시작으로 다양한 방법론들이 나오지 않을까 합니다.
아래의 Loc-NeRF 데모영상으로 마무리하겠습니다.
