[paper review] Unifying Short and Long-Term Tracking with Graph Hierarchies 논문 리뷰

안녕하세요. 이번 포스팅은 Unifying Short and Long-Term Tracking with Graph Hierarchies, 줄여서 SUSHI라는 tracking 모듈을 리뷰하겠습니다.

보통 tracking에서 long-term association, short-term association으로 나뉘는데 본 논문은 두가지의 시나리오를 모두 tackle하였습니다. short-term association이라함은 말그대로 짧은 시간에서 하는 association으로 position을 보통활용하기 때문에 motion model을 만들어서 filter기반으로 association을 수행합니다. (i.e. bytetrack). long-term association의 경우 occlude심할때 꽤 오랜 frame동안 object가 detection이 안될때 발생할 수 있습니다. 이 경우 다양한 방법론이 있을 수 있지만 GNN(graph neural net)을 사용하는 경우가 많습니다. 이 때문에 filter기반의 tracking 모델들을 long-term task를 수행하기 위해 독립적으로 reID 메커니즘을 사용합니다. 

 

*re-ID란?

한 프레임에서 본 객체를 다른 프레임에서 다시 식별하는 테크닉입니다. 보통은 CNN base model을 활용해서 image를 encoding해서 객체를 feature embedding합니다. 이 후에 cosine similarity, Euclidean distance등을 활용하여 유사도를 비교해 가장 ID를 할당합니다. 

 

*GNN에 대해서는 아래 포스팅 참고하세요

[ML] GNN 훑어보기

 

METHOD

SUSHI는 TBD방식으로 detection과 tracking을 분리한 방식이며 tracking만을 다룹니다. detection의 결과를 graph의 vetex로 하고 association을 edge로 치환합니다. association은 multi-cuts, minimum cliques, disjoint path, efficient solvers등이 있는데 여기서는 min-cost flow formulation방식을 사용합니다.

 

 

*min-cost flow formulation이란?

$G=(V,E)$라는 graph에서 각각의 $edge(u,v)$에서 flow를 보낼때 전체의 cost가 최소가 되게 하는 flow를 찾는 문제입니다.$min \sigma c_{ij}f_{ij}$. 보통 LP(선형계획법)을 이용해서 풉니다.

import networkx as nx

# directed graph
G = nx.DiGraph()

# 각 edge에 capacity와 cost 부여
G.add_edge('S', 'A', capacity=15, weight=4)
G.add_edge('S', 'B', capacity=8,  weight=4)
G.add_edge('A', 'B', capacity=20, weight=2)
G.add_edge('A', 'T', capacity=10, weight=2)
G.add_edge('B', 'T', capacity=15, weight=1)

# demand 지정: source는 -도량, sink는 +도량
G.nodes['S']['demand'] = -20  # 보내야 할 총 유량
G.nodes['T']['demand'] = 20   # 받아야 할 총 유량
G.nodes['A']['demand'] = 0
G.nodes['B']['demand'] = 0

# min-cost flow 계산
flowDict = nx.min_cost_flow(G)

# 결과 출력
total_cost = nx.cost_of_flow(G, flowDict)
print("총 비용:", total_cost)
print("\nflow dict:")
for u in flowDict:
    for v in flowDict[u]:
        if flowDict[u][v] > 0:
            print(f"{u} → {v} : {flowDict[u][v]}")

예시 코드이고 위의 코드를 temporal 정보가 있는 detection으로 바꿔서 edge 연결가능성(cost)를 GNN으로하면 같은 구조가 됩니다.

 

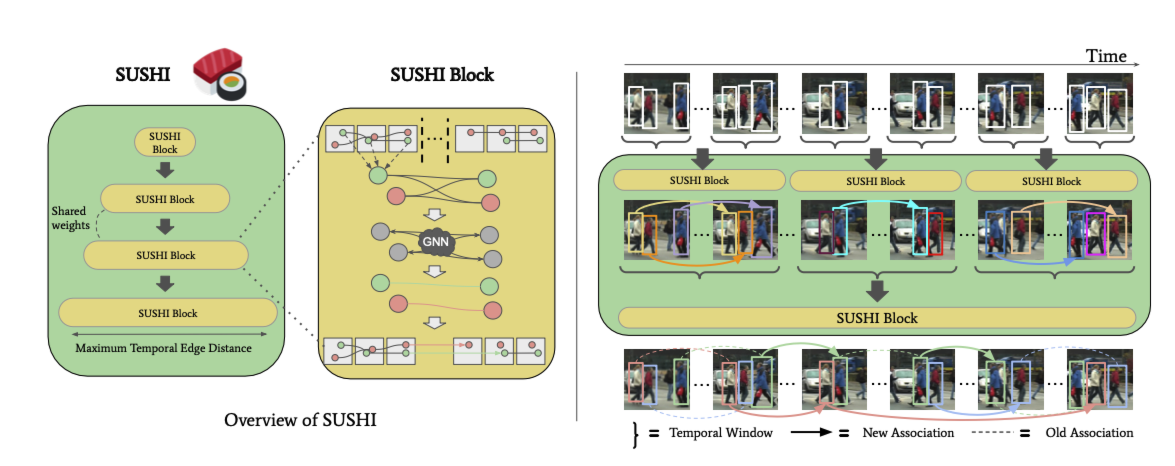
SUSHI의 전체적인 구조는 위의 그림처럼 SUSHI block의 sequence로 이뤄저 있습니다.  즉, hierarchy하게 구조화하여 memory문제를 막고 효율적으로 문제를 풀겠다는 의도입니다.

각 block은 이전의 단계에서 만들어진 tracklet을 입력으로 받고 더 긴 traclet으로 병합해서 내보내는 과정을 담당합니다. 이런 SUSHI block을 쌓아서 반복하면 결국 비디오 전체 길이에 해당하는 완성된 track을 얻을 수 있습니다.

 

SUSHI block

각 block을 살펴보면 node(tracklet)은 위치, appearance, motion등의 특성을 담는 embedding을 갖고 있고, edge(trajectory hypothesis)도 두 tracklet을 연결할때의 유용한 정보를 embedding으로 갖고있습니다. 이를 GNN을 이용해서 msessage passing을 수행합니다. message passing을 거치면서 얼마나 유용한 정보인지가 업데이트 됩니다.

*message passing이란 GNN에서 node들이 정보를 교환하면서 자신의 embedding을 업데이트하는 과정을 말합니다.

 

Limitations of monolithic tracking graphs

하나의 그래프를 사용하면 최대$O(n^{2})$의 edge개수가 필요합니다. 실제로 GT의 경우 각 node는 최대 2개의 edge가 필요하다는 것을 가정할때 최대 $2n$개가 필요합니다. 즉, label imbalance문제가 발생하면서 computation cost뿐아니라 오히려 학습에 악영향을 끼칩니다. 그래서 제안한 hierarchical 방법을 보면 서로 겹치지않는 구간(10~20 frames)로 나누고 각 구간에서만 tracklet을 만들고 edge를 고려하기 때문에 graph의 크기는 매우 작아서 $O(n^{2})$의 문제가 완화될 수 있습니다. 이후에 상위 레벨에서 더 다시 병합시키는데 상위레벨로 가도 (고려할 time span이 더 커도) 이미 하위 레벨에서 노드결합을 해놨기때문에 실제 고려할 node개수는 상대적으로 적어집니다.

 

Learning a unified hierarchical tracker

디테일을 살펴봅시다.  sushi block의 process flow를 단계별로 보면 처음에 graph를 구성합니다. tracklet을 node로 설정하고 edge를 만들어 해당 level에서의 graph를 생성합니다. $G^{l} = (V^{l}, E^{l})$

다음으로 message passing단계인데, node embedding, edge embedding의 intialization하고 GNN을 통해 임베딩을 업데이트합니다. 이후 classifier(mlp)를 통과해서 잘연결이 되었는지 판별하고 올바른 연결이라고 판별된 엣지로 연결과 node를 병합하고 상위 level에 사용할 수 있도록 tracket을 생성합니다.

그 과정에서 embedding에 사용하는 edge association cues는 appearance embedding, motion feature, temporal proximity를 사용합니다. 그리고 GNN는 shared weight이고 level마다 jointly training을 하고 초기에는 level 1만 unfreeze하면서 점차 높은 레벨까지 unfreeze하는 식으로 진행합니다.

 

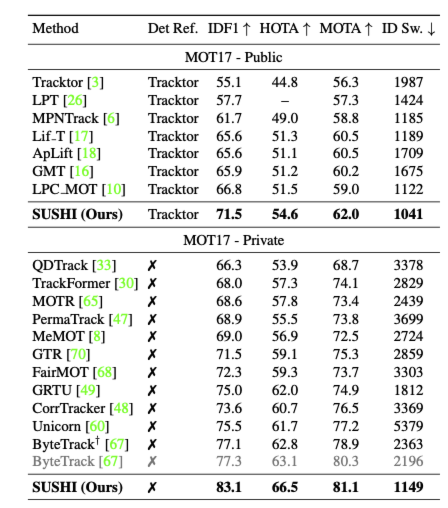
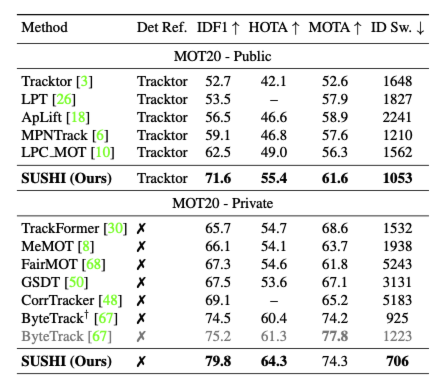
experiments

사용되는 metric에 대해서 간단히 설명하면

- IDF1 : ID유지를 어느 정도로 잘했는가. Identity preservation입니다. ID바뀌면 점수가 깎입니다.(association위주)

- MOTA : detection성능에 많이 의존됩니다.

- HOTA : detection, association, localization을 균형있게 합쳐놓은 metric입니다.

- ID sw : ID switching된 지표입니다.