[paper revew] pointnet 논문 리뷰

이번 포스팅은 3D pointcloud detection의 고전 pointnet를 보겠습니다.

 

PointNet

pointnet은 딥러닝을 사용한 pointcloud detection 분야의 고전으로 현재 많은 알고리즘의 토대가 되는 논문입니다. 우선 3D pointcloud의 성질부터 이해할 필요가 있는데, unordered point set이라는 점입니다. image는 픽셀이라는 정해진 discrete한 공간에 있다면 pointcloud는 유클리드 공간이라는 continuous한 공간에 있습니다. 그래서 많은 다른 알고리즘들이 voxel grid를 만들어서 마치 image처럼 처리를 합니다. 즉, pointcloud를 뉴럴넷으로 detection문제를 해결하기 위해서는 1. unordered 2. interaction among points 3. Invariance under transformation 이렇게 3가지를 해결해야 합니다. pointnet은 위의 문제를 어떻게 풀었는지 살펴보겠습니다.

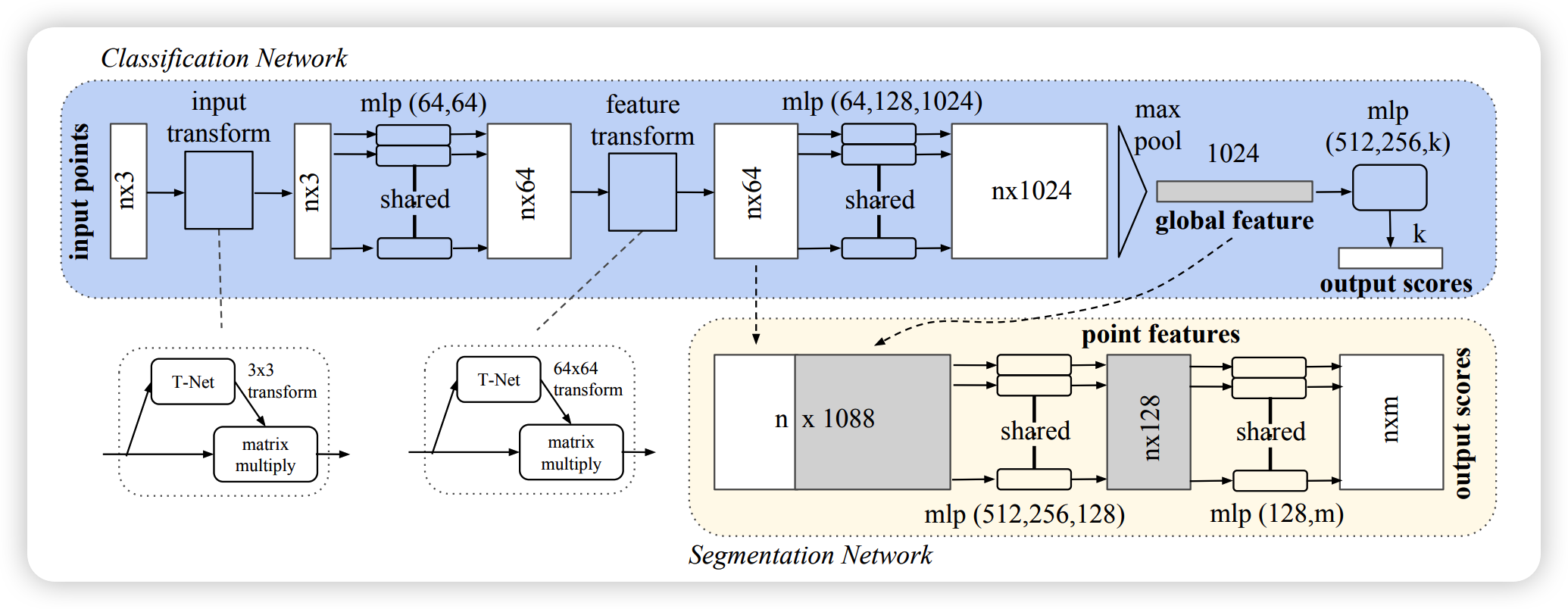
위의 그림은 pointnet의 overview입니다. 사실 매우간단해서 model에 대해서는 설명할것이 거의 없습니다. point(x,y,z)가 MLP로 몇단계를 거쳐서 max pooling과 activation function을 통해 score를 뽑아 classification 혹은 point단위로 masking(segmentation)하는 것이 전부입니다. 아래는 왜 위와 같은 아키텍쳐를 만들었는지 하나하나 보도록하겠습니다.

Symmetry Function for Unordered Input

 unordered문제란, point들이 어떠한 순서로 model에 들어와도 동일한 결과물을 내야한다는 말입니다. 이를 해결하기 위해서는 3가지 방법이 있는데 

 첫번째는, sort 즉, 말그대로 point들을 항상 정렬하는 것 입니다. 어떤 표준적인 조건을 만들고 그 규칙에 맞춰 항상 sort해서 model에 입력시키는 방법입니다. 하지만 이 방법은 High dimension으로 가면 사실상 사용하기 불가능 합니다.

 두번째는, RNN을 적용하는 것입니다. 하지만 이 방법도 마친가지로 문제가 있는데, small length가 아닌 large size에서는 효과가 없다고 합니다.(refer, OrderMatters). pointcloud는 보통 적어도 몇천개 정도 되니 사실상 적용이 힘듭니다.

 마지막으로 논문에서 제시하는 방법인데요, MLP를 이용하여 approximate general function을 만드는 것입니다.

general function

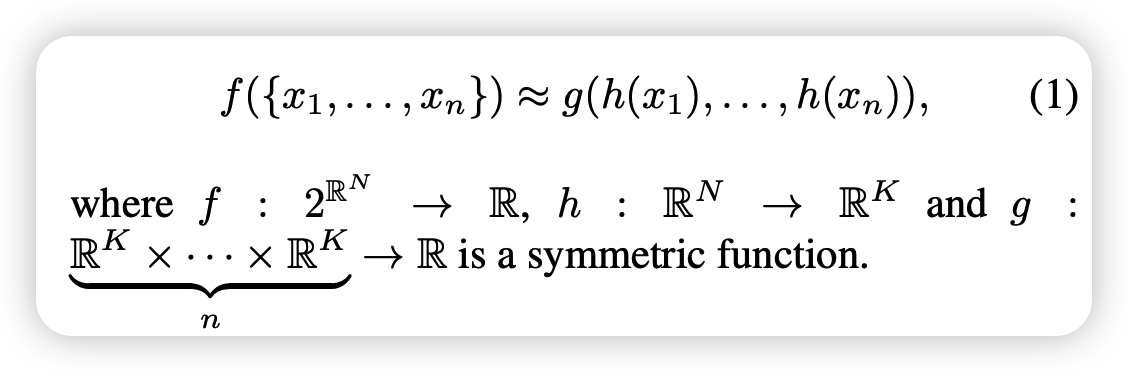
h함수는 mlp로 이루어진 뉴럴넷이고 g함수는 max pooling function을 뜻합니다. overview그림을 참고하세요.

실제 문제에 적용해보면 point n개가 mlp로 이루어진 function에 input으로 각각 들어가고 output으로 나온값들은 max pooling합니다. 이렇게 되면 어떤 순서로 point가 model로 들어가더라도 max pooling을 통해 나오는 값은 동일합니다. 즉, 이를 통해 unoredered문제를 해결할 수 있습니다.

 

Local and Global Information Aggregation

  interaction문제란, 포인트들 서로간의 연관성을 뜻합니다. locally하게 볼 수도 있고 globally하게 서로간의 관계를 파악할 수도 있습니다. 사실 classification의 경우 MLP, global max pooling등을 통하면 global interaction 문제해결을 포함한 것과 같습니다. 하지만 segmentation의 경우 local과 global간의 combination이 필요합니다. 이를 위해서 segmentation은 MLP를 통해 나온 Feature와 max pooling을 통해 나온 global feature를 concat하여 사용합니다.

concat

 Joint Alignment Network

마지막으로 세번째 문제인 invariance under transformation이라 함은 object가 거꾸로 있거나 구석에 있어도 그와는 불편하게 동일한 성능을 유지한다는 것을 의미합니다. 이를 해결하기 위해서 mini-network(T-net)를 도입합니다. 

T-net

feature space의 T-net은 higher dimension을 다루기 때문에 regularization을 추가하였다고 합니다.

regularization

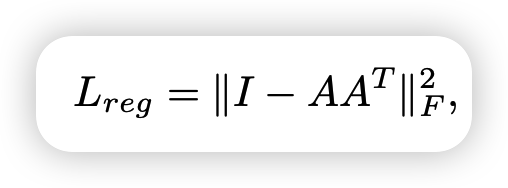
Theoretical Analysis

 각각의 point들에 mlp과정을 거쳐서(+ T-net) global pooling으로도 꽤 높은 성능을 보이는 이유로 논문에서는 단순 실험결과 뿐아니라 이론적으로도 근거를 제시했습니다. 

general function

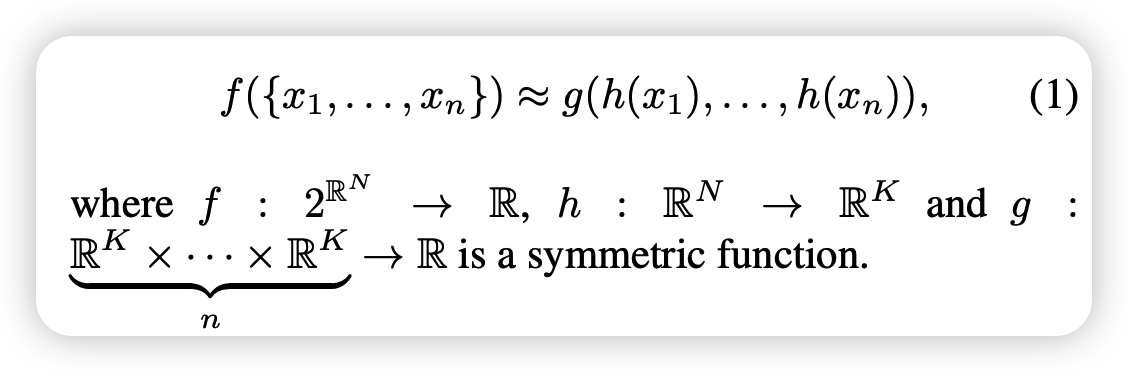
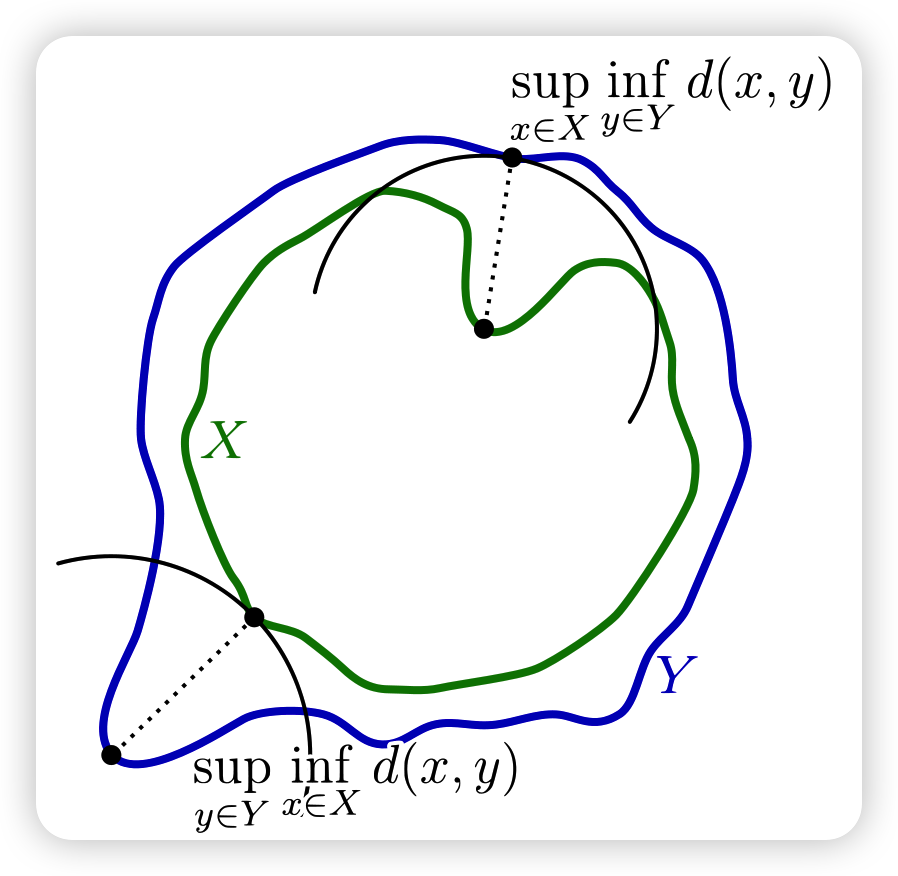
위의 식은 앞서 설명한 general function을 mlp와 max pooling으로 approximate한 식입니다. 이것이 성립할 수 있다는 근거로 아래의  Hausdorff distance라는 이미 수학적으로 증명된 식을 제시합니다.

Hausdorff distance

충분히 많은 $\alpha$가 있을때 (point들이 있을때) Hausdorff distance의 max값 (global max pooling)은 general function과 $\epsilon$(매우작은) 차이밖에 나지 않다는 뜻입니다.

Hausdorff distance

Experiments

 

unordered

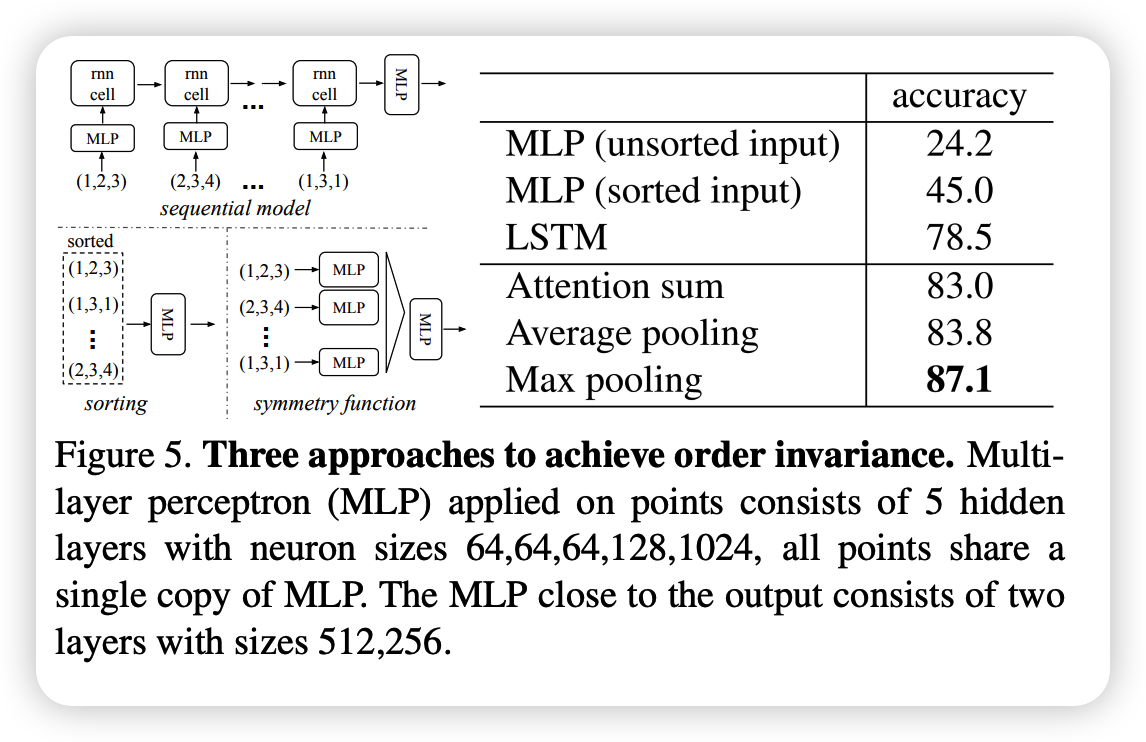
unordered point를 처리하는 방법으로 위에 sort, RNN방법도 말씀드렸습니다. 위의 실험은 그 방법들의 성능이고 논문에서 제시한 general function방법 대비 성능이 매우 떨어집니다.

T-net

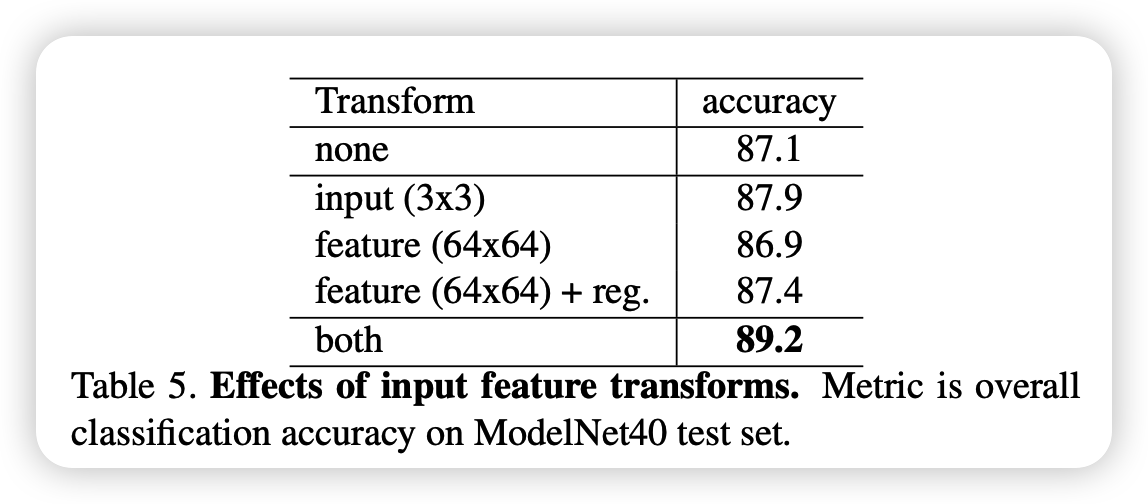
transform에 invarient한 모델을 만들기 위해 T-net을 추가했었는데 그에 대한 성능 입니다. 매우 큰 영향을 끼치지는 않는 것 같습니다.

benchmark

output

성능 결과입니다. 사실 pointnet이 나온지 꽤 오래되서 이미 훨씬 더 성능이 좋은 모델들이 많지만, 저때의 비슷한 모델들 대비 엄청난 성능 증가가 있는 것을 알 수 있습니다.

---

pointnet이 최근 pcd 기반 3D detection의 기본이 되는 모델이다 보니 추후 관련 논문을 읽기 위해라도 한번은 훑고 지나가는게 좋을 것같습니다.