[paper review] Nerfies: Deformable Neural Radiance Fields 리뷰

안녕하세요. 후니대디입니다.

이번 포스팅은 Nerfies 논문 리뷰 진행하겠습니다.

NeRF의 기본적인 개념은 아래의 포스팅 참고바랍니다.

[paper review] NeRF 논문 리뷰

---

overview

overview

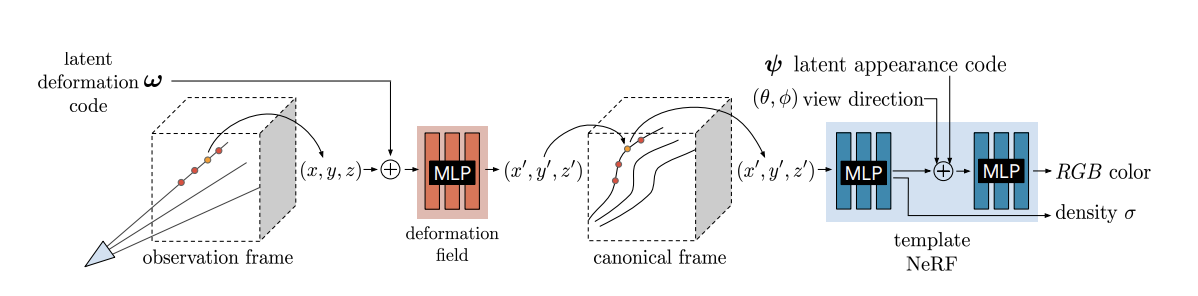
 기존의 vanilla NeRF의 문제점 중 하나는 object가 고정되어 있어야 합니다. 장난감이나 고정되어 있는 object면 상관없지만 만약 내 모습을 여러 각도에서 셀카를 찍어 Novel View를 만들고 싶다고 했을때, 아예 움직이지 않고 셀카를 찍기에는 불가능합니다. Neries는 기본적인 NeRF flow에서 deformation field를 통한 canonical frame을 만들어서 움직이는 object의 novel view를 잘 표현할 수 있다는 것에 목적이 있습니다.

 object의 deformation(의역하면 움직임)에 robust해지기 위한 방법으로 canonical frame을 도입하고 explicit하게 매핑하는 것이 아닌 MLP를 통해 implicit하게 canonical frame으로 매핑하여 deformation을 해결합니다. 그 외에도 여러 technic들이 있는데 아래에서 살펴보겠습니다.

 

---

Neural Deformation Fields

 위에 언급한 deformation field에 대해 설명하겠습니다. NeRF의 기존 알고리즘과 같이 pixel ray을 쏴 point를 sampling하고 sampling된 point들의 pose와 latent code(w)를 concat하여 MLP로 구성된 deformation field를 통해 canonical frame상의 position을 뽑아냅니다. (observation frame에서의 pose는 NeRF와 마찬가지로 SfM등을 통해 미리 알고 있어야합니다.)

이를 식으로 표현하면 다음과 같습니다. point의 position과 latent vector를 input으로 하여 deformation function을 통해 canonical frame상의 position을 출력하고, 그 값과 direction 그리고 appearance latent vector를 input으로 하는 MLP function에 input으로 들어가게됩니다.vanilla NeRF와 다르게 appearance latent가 추가됩니다. 이는 NeRF-W에서 나온 기법인데 exposure와 white balance를 반영키위함 입니다.

observation-space eq

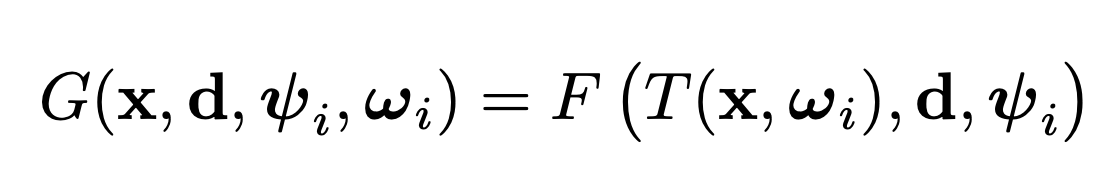
 위 eq에 T에 해당하는 deformation field에 대해 좀 더 구체적으로 보면 논문에서는 displacement field방법과 SE3를 설명합니다.

displacement field는 simple한 방법으로 observation field에서 canonical frame으로 매핑하는 방법이 단순 translation으로 이루어집니다.

displacement field

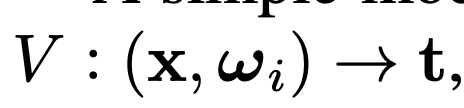
 SE3 field는 이전에 포스팅했던 Lie Group을 이용한 변환방법입니다.

[SLAM] 2.리군, 리대수(Lie Group, Lie Algebra)

간략하게 설명하면, observation coordinate -> cononical coordinate으로 매핑하는 최적의 se3상의 r,v(6차원 벡터)를 설정합니다. MLP를 통해 최적화를 하여 최적의 r,v를 구하고 exponential map 연산을 통해 SE3상의 R|T값을 구하게 됩니다.

so3 exponential mapping eq

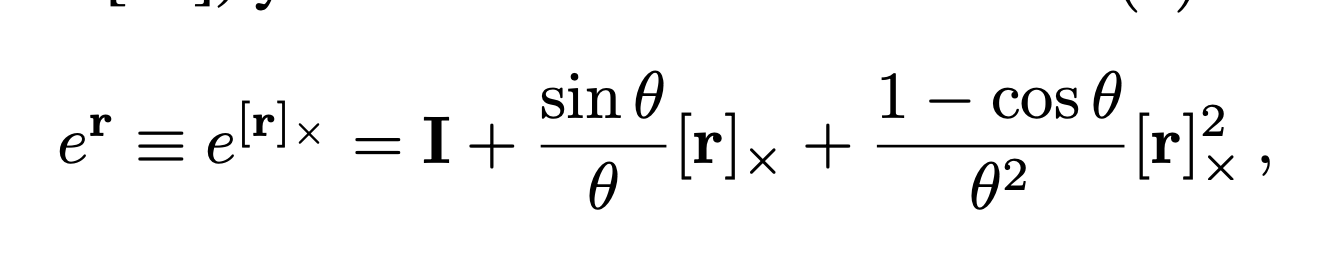
위의 식은 so3의 exponential map 연산으로 rodrigues 공식입니다. 여기에 translation부분까지 연산에 추가하여 아래와 같이 se3의 exponential map 연산을 구할 수 있습니다.

se3 exponential mapping eq

최종 tranformation eq

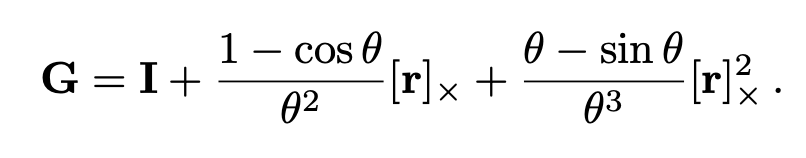
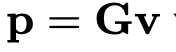
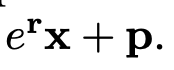
Lie Group을 이용한 변환의 장점은 Lie Group포스팅에서 보시면 되겠습니다.

---

Elastic Regularization

elastic picture

 위의 사진을 보시면 elastic off의 경우 코와 안경등의 모양이 부자연스러움을 알 수 있습니다. 이는 2D 사진에서는 물체가 앞뒤로 움직이는 것과 커지거나 작아지는 것과 동일하게 표현되기 때문입니다. 일종의 scale ambiguity와 같습니다. 이를 방지하기 위해 elastic energy라는 방법을 사용합니다. 기본 컨셉은 어느 한 픽셀 혹은 포인트의 deformation과  주변의 그것이 비슷해야한다는 가정입니다. 이를 위해 자코비안을 활용합니다. 자코비안은 벡터나 행렬에서의 각각 파라미터로 편미분한 계수인데, 즉 해당 위치에서의 기울기 혹은 변화량을 의미합니다.

자코비안을 SVD로 decomposition하여 singular value를 제외한 두 행렬의 곱을 통해 R행렬을 얻고 자코비안과 R의 차이를 loss function으로 정의합니다. 아래식을 참고해주세요.

svd 자코비안

 

loss function

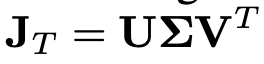
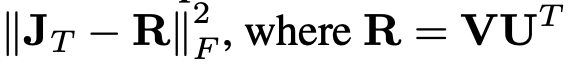
위의 loss function에 log를 취하면 ( log는 최대 최소에 영향을 주지않으므로 ) 아래와 같이 간략화 시킬수 있고 singular value log값의 L2 norm으로 loss function을 정의 할 수있습니다.

loss function of elastic

 정리하면 observation field -> canonical field로 매핑하는 과정에서 구한 자코비안의 SVD중에 sigular value 값을 최소로 하게 하는 파라미터를 찾는 것인데, 기하학적으로 고민해보면 SVD에서 U,V는 회전을 나타내고 sigular value는 각 축에 대한 scale을 나타냅니다. 찌그러지는 정도를 나타낸다고 볼 수 있죠. 즉, 위의 elastic loss는 local한 반경에서 최대한 절 찌그러지는 방향으로 deformation하는 목적이 아닐까 추측합니다.- 이에 대해 자세히 알고 계시면 댓글부탁드립니다 :) -

자세한건 elastic energy관련 paper를 읽어보시기를 추천드립니다.

 

 이렇게 구한 elastic loss에 robust loss를 적용합니다.

robust loss

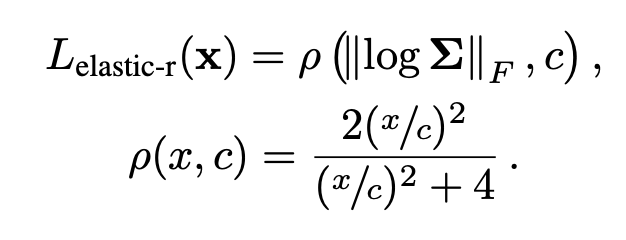
Geman-McClure robust function이라고 하는데요. 아웃라이어를 제거하기 위함입니다. 즉, local한 영역이 무조건 비슷한 성격을 따르지 않을 수도 있기 때문입니다. 예를 들면 얼굴과 배경사이의 영역은 인접하지만 다른 성격을 가지고 있죠. 

방법은 loss가 일정 이상 크면 무시해주거나 weight를 낮게 주는 것 입니다.

---

Background Regularization

 보통 백그라운드는 deformation하지 않습니다. 벽이 움직이지는 않죠. 이를 위해 백그라운드 points들은 regularization을 해줍니다.  loss가 사실상 0입니다. 

background regularization

 

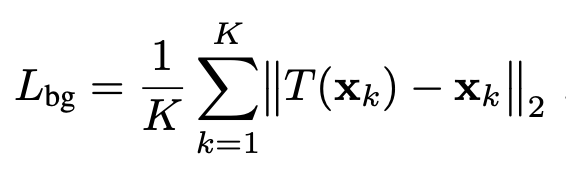
DeepLabV3 segmentation 모델을 masking해서 백그라운드를 판단합니다.

---

Coarse-to-Fine Deformation Regularization

NeRF와 마찬가지로 position encoding을 거칩니다. 여기서 추가되는 부분은 annealing과정을 거치면서 frequency를 줄여줍니다.

Coarse-to-Fine Deformation Regularization

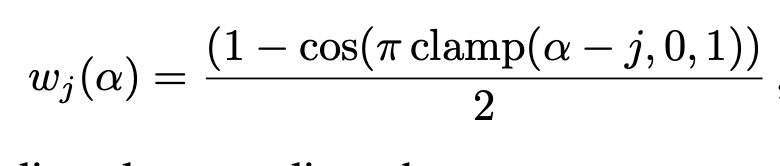
해당 regularization을 적용하는 이유는 frequency가 낮으면 under-fitting이 높으면 over-fitting이 되기 때문에 해당 방법을 이용했다고 합니다.

 

---

MLP model

mlp model은 딱히 설명할 건 없습니다. 아래와 같고 latent vector과 활용되는 것이 이전의 NeRF와 다른 점 입니다.

deformation mlp

nerf-w mlp model

---

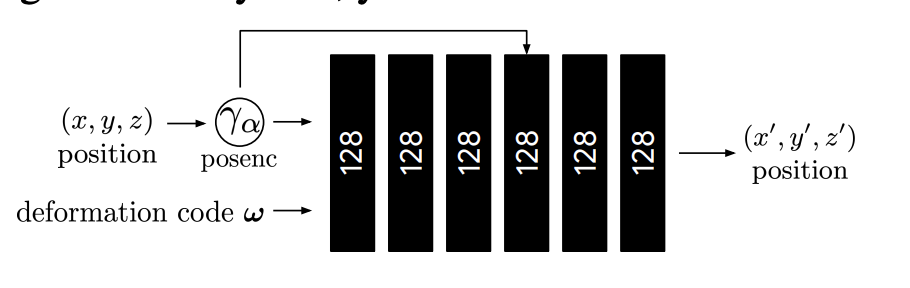
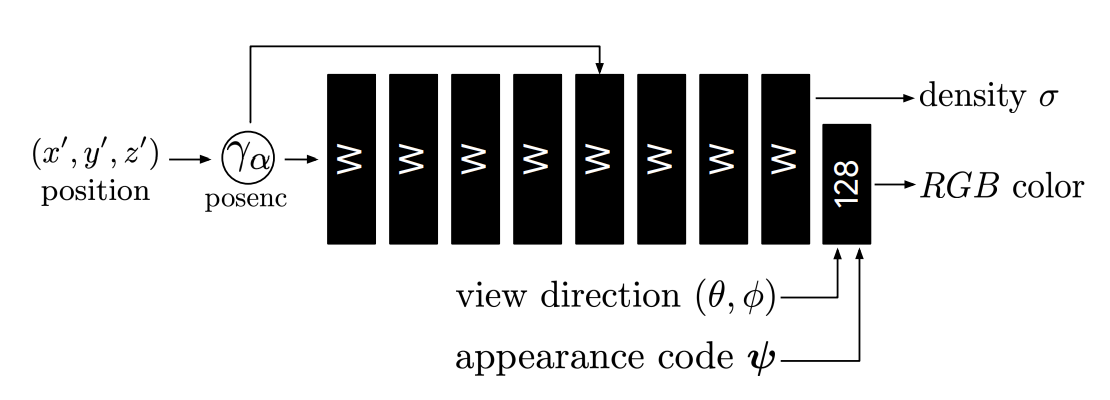
Experiments

rig

실험방법이 특이한데 위의 사진과 같이 rig에 좌우 카메라를 달고 왼쪽은 트레이닝용 오늘쪽은 테스트용으로 활용하였습니다.

 

dynamic

dynamic scene 실험결과입니다.

quasi-static scene

약간의 움직임이 있는경우 실험결과입니다.

ablation study

ablation study결과입니다. dynamic 씬에서는 elastic이 중요한데 움직임이 별로 없는 씬에서는 매우 큰 영향을 주지는 않는 것 같습니다.

 

---

conclusion

아래는 nerfies 발표영상과 결과물 동영상입니다. 보면 매우 결과물이 좋습니다. 특히 novel view depth는 어마어마합니다..  하지만 학습의 오랜시간과 빠른 움직임에는 학습이 되지 않는 단점을 가지고 있다고 합니다.

이상으로 리뷰 마칩니다 :)