[paper review] AB3MOT 리뷰, 3D Multi Object Tracking

이번 포스팅은 AB3MOT라는 3D Multi Object Tracking 논문을 리뷰하겠습니다.

'AB'라는 의미는 3D MOT의 baseline이라는 느낌을 주기 위해 지은 이름이라고 추측됩니다 ;

---

Intro

 

3D MOT

위의 표는 MOT관련하여 정리한 내용입니다. tracking하는 방법은 접근 방법에 따라 크게 TBD, JDT, Transformer-based 로 나눌 수 있습니다.(제가 임의로 나눈것입니다;;) 2D 에서 tracking의 baseline인 SORT알고리즘이 TBD에 해당하는데 이는 detector를 따로 두고 나온 bbox를 input으로하고 association방법을 추가하여 tracking모듈을 만듭니다. 그렇기 때문에 detector의 성능에 의존성이 있고 전체적인 아키텍쳐가 좀 커집니다.

JDT는 detector부분과 tracking부분이 한덩어리로 하여 end-to-end로 학습하는 방법을 보통 말합니다. 그렇게 때문에 학습을 따로 할 필요가 없습니다. Trasformer방법은 3D에서 아직 보지 못해 적지 않았습니다.

TBD, JDT방법 모두 전체 아키텍쳐 안에 detector와 association부분이 있습니다. TBD같은 경우 위에 말했듯이 detector를 기존 모델을 사용하고 나온 결과물을 가지고 KF를 사용하여 accociation을 진행합니다.이 방법이 이 포스팅에서 설명할 AB3MOT방법입니다.

JDT같은 경우는 association부분도 learning base로 이루어져야 하기때문에 RNN의 sequencial한 network 혹은 trasnformer를 활용하여 accociation을 진행합니다.

 

Kalman Filter

KF

다음으로 배경지식을 위한 KF를 살펴보겠습니다. Kalman Filter는 칼만 선생님이 세상에 내놓은지 오랜시간이 지났지만 아직도 많은 영역에서 사용됩니다. 칼만필터의 큰 그림을 말씀드리면 보통 어떤 값을 예측할때 많이 쓰입니다. 예를 들면 자동차의 현재위치를 예측한다고 하였을때 칼만필터를 사용하기 위해하는 두 개의 시스템을 정의해야합니다. 예컨테 imu 센서를 이용하여 운동 방정식 시스템을 설계합니다. 즉, imu의 가속도 값을 이용해 현재의 위치를 추정할 수 있는 시스템을 하나만듭니다(시스템1). 이번엔 GPS를 통해 현재 위치를 알수 있는 관측 시스템을 설계합니다(시스템2). 센서와 정의한 시스템에 noise가 없다면 시스템1과 시스템2의 결과(현재위치)는 같아야 합니다. 하지만 실제의 세상은 온갖 noise로 가득하기에 시스템1과 시스템2에서 나온 결과(위치)는 같을 수가 없죠.

이럴때 칼만필터를 사용하여 시스템1과 시스템2의 결과를 fusion하여 최선의 결과(위치)를 예측할 수 있습니다. 

여기서 언급한 fusion의 방법론 중 하나가 바로 칼만필터입니다. 두 시스템의 covariance를 이용하여 adaptive하게 중요도(칼만게인)을 구하고 convolution하여 최선의 결과를 예측합니다. 정답은 아닐 수 있어도 최선의 예측이라는 것이 수학적으로 증명되어있습니다.

또한 칼만필터는 시스템이 선형일때만 쓰일 수 있고 선형이 아닐때는 확장칼만필터(EKF;테일러 급수로 approximation)를 통해, noise가 가우시안 distribution이 아니면 UKF나 PF를 통해 fusion할 수 있습니다.

 

Detector

 

detector

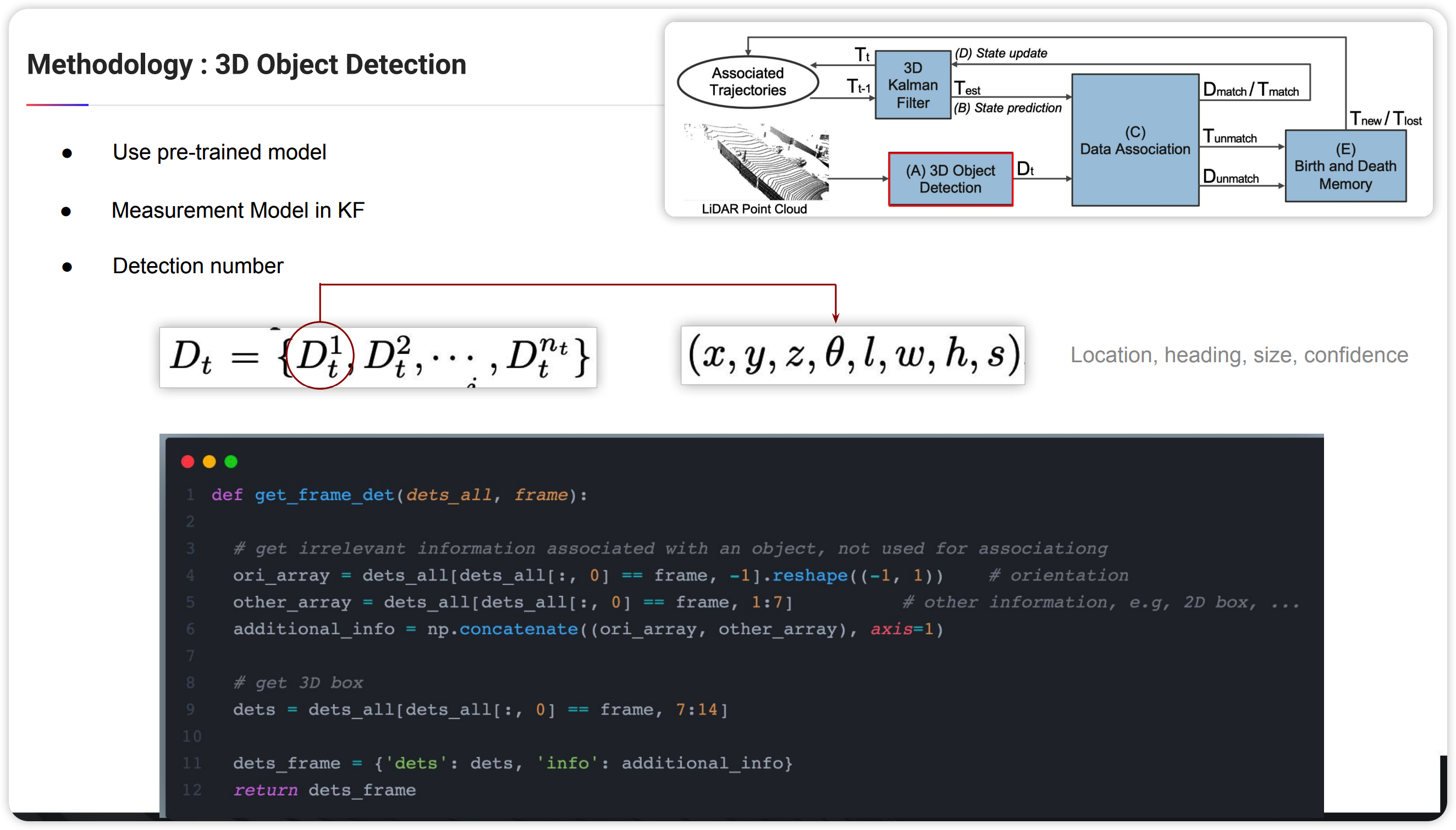
본격적으로 AB3MOT의 알고리즘을 살펴보겠습니다. 위에 그림은 우선 detector로 부터 예측되는 Object의 bbox를 가져오는 부분입니다. 공개 코드에서는 detector로 pointrcnn을 사용하였습니다.

이 부분이 앞서 설명한 KF에서 시스템2에 해당합니다. 즉 detector를 통해 나온 object의 위치 및 bbox의 크기가 측정 시스템이 되는 것 입니다.

[paper review] pointRCNN 리뷰

 

Prediction

prediction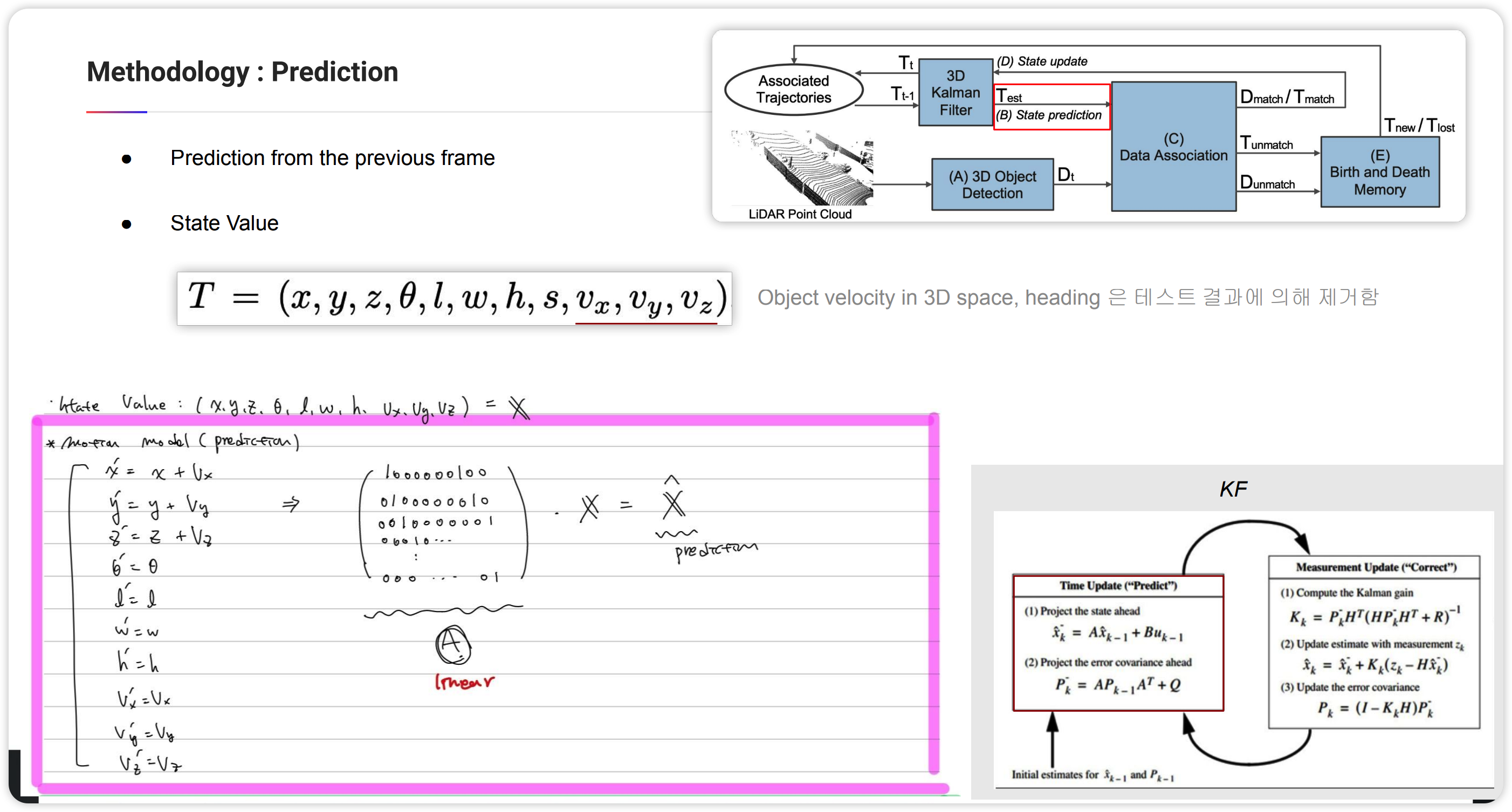

Prediction은 KF를 사용하기 위해 정의되어야 할 시스템1에 해당합니다. 해당 논문에서는 시스템1을 정의하기 위한 constrain으로 해당 object의 속도가 일정하다는 가정을 두었습니다. 그리고 구할 state value로는 해당 object의 위치와 헤딩각도 ($x, y, z, \theta $),bbox의 크기($l, w, h$) 그리고 속도($v_x,v_y,v_z$)입니다.

이를 이용하여 시스템1을 정의하면 위의 분홍색 박스와 같이 됩니다. 즉 time domain에서  state value의 다음 값을 주어진 constrain을 이용해서 예측하는 것입니다. 여기서는 '속도가 일정하다'라는 부분이 되겠죠.

이렇게 시스템1이 완성되었습니다.

prediction code

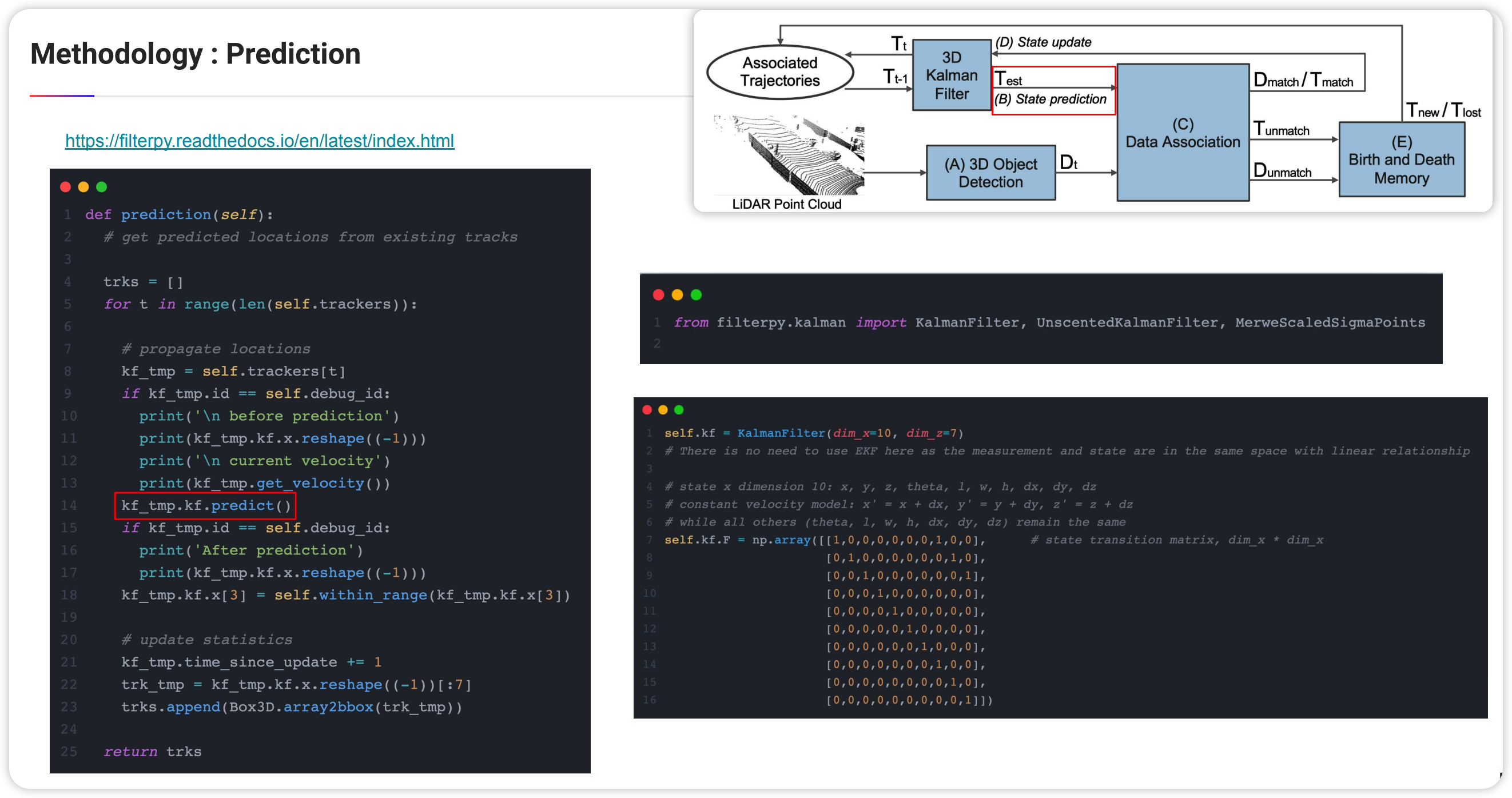
위의 그림은 prediction을 코드로 어떻게 구현하였는지를 본 것 입니다. 공식 코드에서는 kalman filter 구현을 pyfilter라는 라이브러리를 사용하여 보다 쉽게 구현하였습니다.

$self.kf.F$부분은 위에서 설명한 시스템1을 구할때 나온 A와 같습니다.

 

association

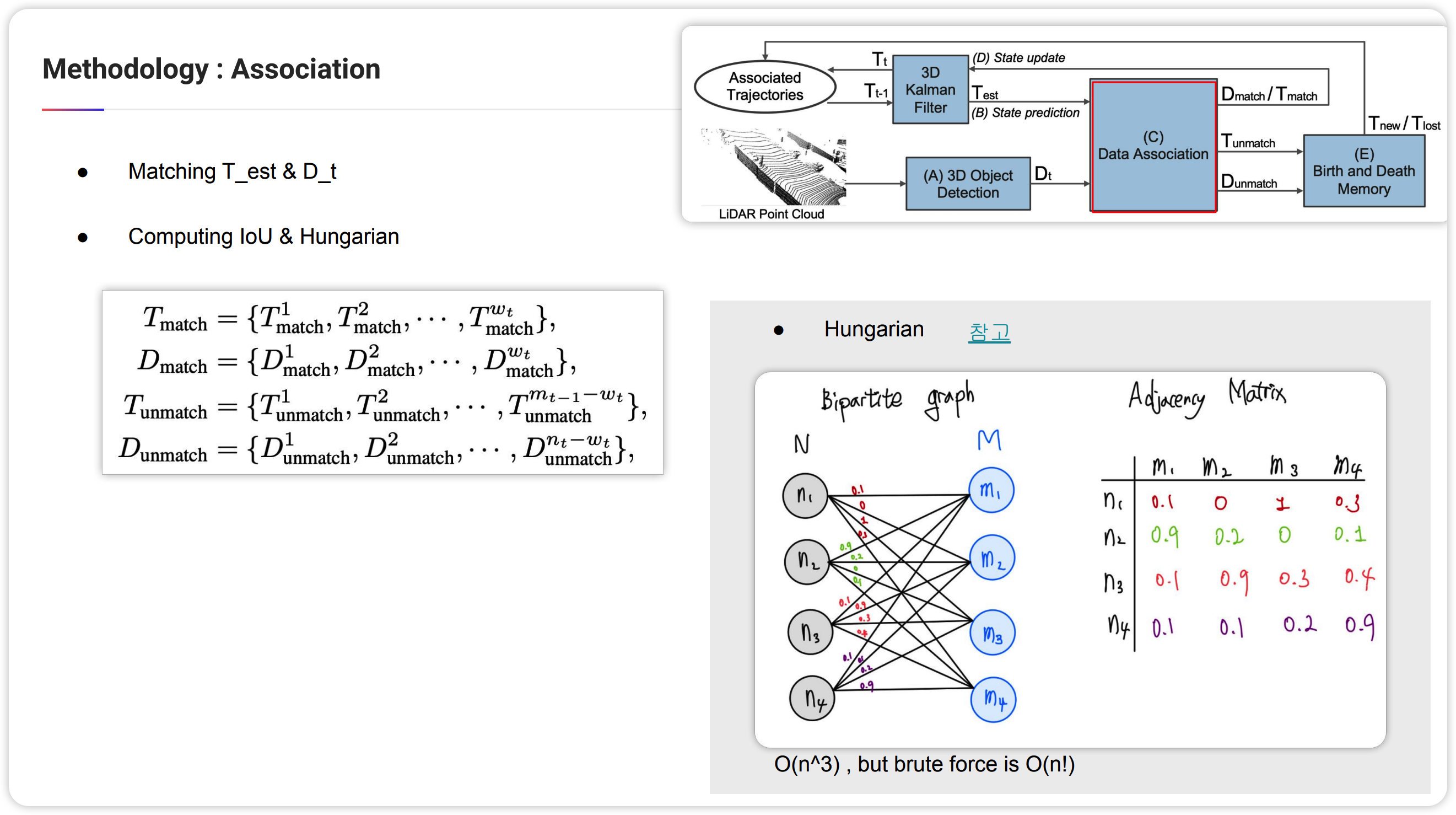
Association은 KF와는 관련이 없지만 tracking에서는 핵심인 부분입니다. 만약 하나의 object를 tracking한다면 association하는 부분이 필요가 없습니다. 하지만 multi object의 경우에는 detector를 통해 구한 object와(시스템2) prediction을 통해 구한 object(시스템1)의 매칭을 찾아야합니다. 즉 같은 object끼리 짝지어 fusion을 해야한다는 말입니다. 이를 위해 논문에서는 Hungarian알고리즘과 IoU를 사용합니다. 

즉 시스템1에서 나온 bbox와 시스템2에서 나온 bbox의 IoU를 비교합니다. 모든 경우의 수를 비교하면(brute force, $O(n^3)$) 비싸니 헝가리안 알고리즘을 활용($O(n!)$)하여 비교합니다.

그렇게 되면 매칭이 되는 bbox들과 매칭이 되지 않는 bbox들이 나오게 됩니다. (매칭이 되지 않는 bbox들은 나오지 않을 수도 있습니다-모든것들이 완벽하게 되었다면..;)

위의 노테이션은 매칭된 예측시스템의 결과물(시스템1)을$T_match$, 매칭된 측정시스템(시스템2)의 결과물을 $D_matrch$로 표현한 것 입니다.

Association code

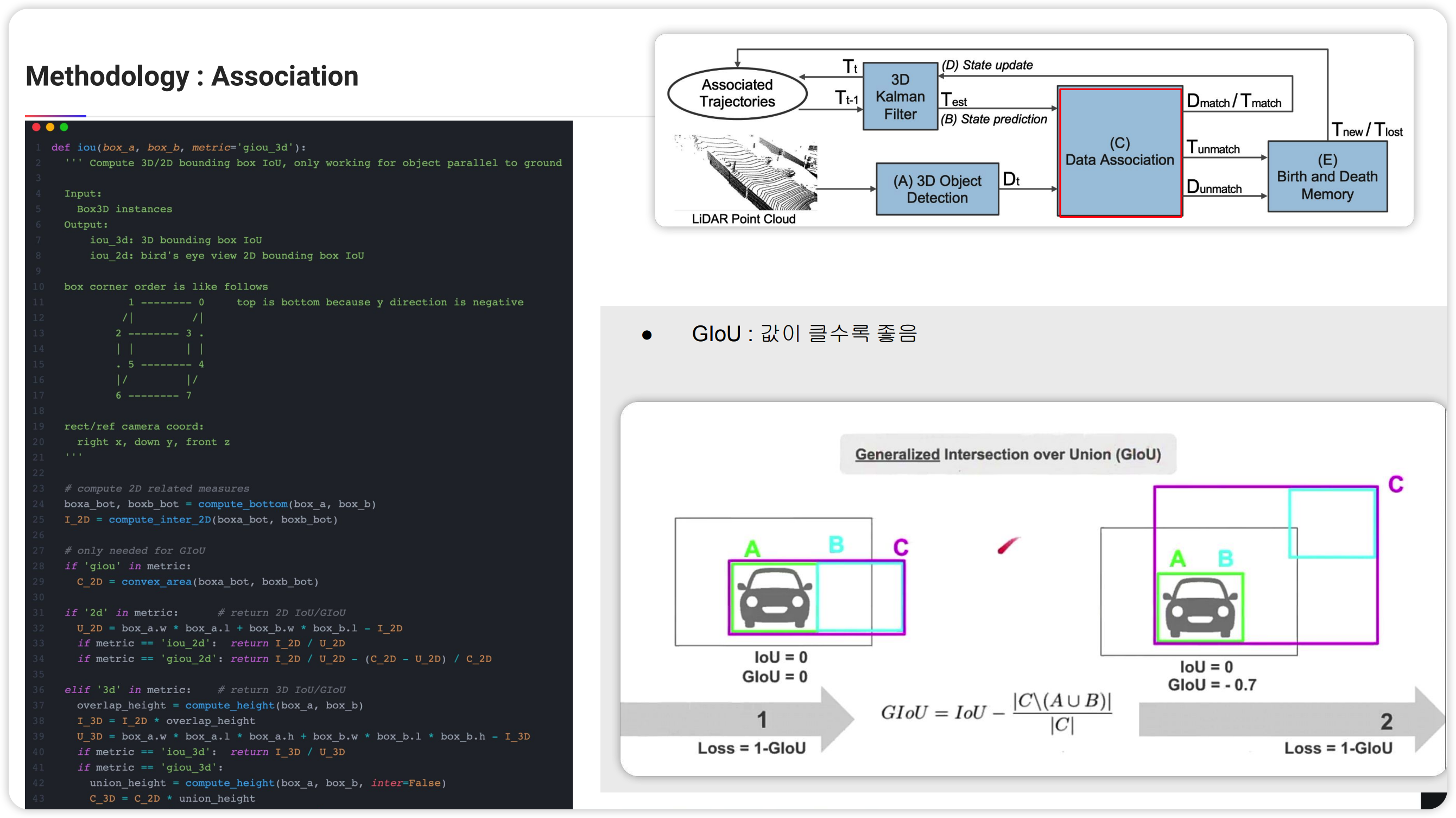
Association 부분의 코드입니다. 공식 코드는 업데이트 되어 단순 IoU가 아니라 GIoU를 사용하였는데 겹치는 부분이 없었을 때도 그것을 수치화 하기 위함입니다. 즉 bbox가 겹치는 부분이 없으면 IoU는 무조건 0밖에 표시할 수 없지만 GIoU같은 경우 더 멀리 떨어져 있으면 음수로도 표현 될 수 있습니다.

Updata

update

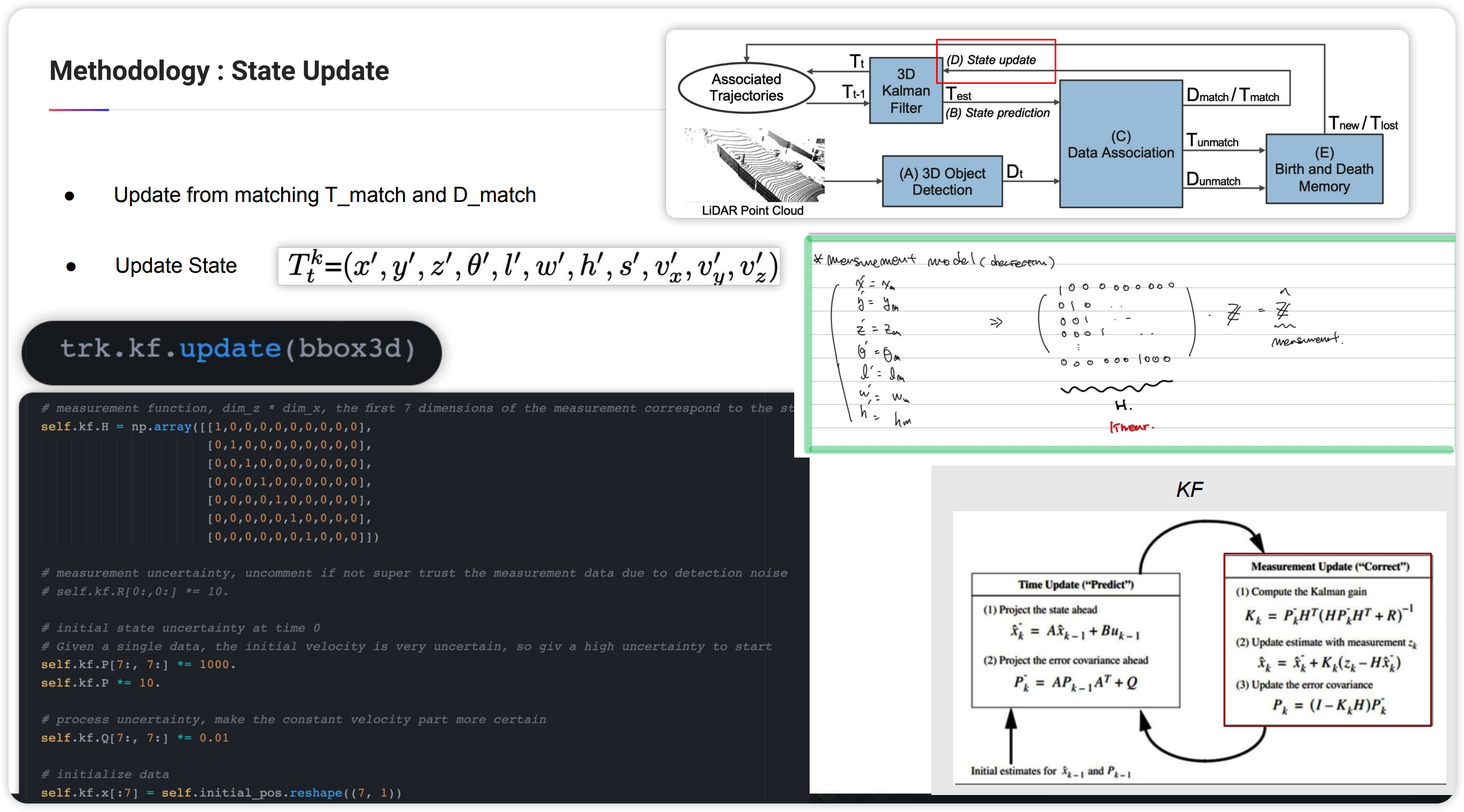
update는 위에서 언급한 fusion에 해당합니다. 즉 시스템1과 시스템2을 구하였고 또 association부분에서 매칭되는 시스템1, 시스템2의 쌍을 구하였습니다. 이를 KF 알고리즘에 녹여서 최적의 예측값을 구하는 부분입니다. 사실 칼만필터 공식에 넣는 부분이라 구하는 것 자체는 어렵지 않습니다.

혹시 칼만필터의 유도가 궁금하신 분들을 아래 참고해주세요.

Master Thesis Final.pdf

Birth & Death Memory

memory

마지막으로 birth&death memory부분인데 이 부분 또한 tracking에서 매우 중요한 부분인데 association단계에서 unmatch된 부분을 관리합니다.

$D_unmatch$부분은 detector시스템(시스템2)에서는 관측이 되었지만 예측시스템(시스템1)는 관측이 안됨을 이야기합니다. 이는 두가지로 해석할 수 있는데 하나는 새로운 object이던지 혹은 detection의 false positive인 case입니다.

$T_unmatch$부분은 예측시스템(시스템1)에서는 관측이 되었지만 detector(시스템2)에서는 관측이 안됨을 말합니다. 이 또한 두가지로 해석할 수 있는데 object가 disappear되었던지 혹은 detector의 false negative인 case입니다.

이를 해결하기 위해 memory 모듈에서는 버퍼를 만들어 놓고 카운팅을 통해 실제로 object가 사라지거나 나타났는지 관리합니다. 즉 $D_unmatch$에 특정 object가 처음나타나면 이 object을 새로운 object로 바로 올리지 않고(false positive일 수도 있기 때문에) 버퍼에 넣어 다음 frame까지 기달려서 지켜본 후 판단을 하게 됩니다.

Metric

metric

해당 논문에서 contribution으로 제기한 것 중 하나는 metric을 제안했다는 것인데 이전의 3D MOT의 metric은 MOTA방법으로 detector confidence의 threshold값에 따라 성능값의 차이가 크기 때문에 이를 평균을 내어 보다 정확한 metric을 제안합니다.

사실 MOTA를 average하여 평가하는 것으로 요약할 수 있습니다.

---

여기까지 AB3MOT의 리뷰를 살펴보았습니다. 3D MOT는 사실 많은 paper나 dataset도 부족한 것이 사실이지만 최근에는 그래도 점점 paper들이 publish되는 것 같습니다.